【题目】已知函数f(x)=4cosωxsin(ωx![]() )(ω>0)的最小正周期是π.
)(ω>0)的最小正周期是π.
(1)求函数f(x)在区间(0,π)上的单调递增区间;
(2)若f(x0)![]() ,x0∈[
,x0∈[![]() ,
,![]() ],求cos2x0的值.
],求cos2x0的值.
参考答案:
【答案】(1)(0,![]() ],[
],[![]() ,π).(2)
,π).(2)![]()
【解析】
(1)利用两角和差的三角公式结合辅助角公式进行化简,结合周期公式求出ω的值,结合单调性进行求解即可.
(2)根据条件,结合两角和差的余弦公式进行求解即可.
(1)f(x)=4cosωx(sinωxcos![]() cosωxsin
cosωxsin![]() )
)
=4cosωx(![]() sinωx
sinωx![]() cosωx)=2
cosωx)=2![]() sinωxcosωx﹣2cos2ωx
sinωxcosωx﹣2cos2ωx![]() sin2ωx﹣cos2ωx﹣1=2sin(2ωx
sin2ωx﹣cos2ωx﹣1=2sin(2ωx![]() )﹣1,
)﹣1,
∵f(x)的最小正周期是π,
∴T![]() π,得ω=1,
π,得ω=1,
即f(x)=2sin(2x![]() )﹣1,
)﹣1,
由2kπ![]() 2x
2x![]() 2kπ
2kπ![]() ,k∈Z
,k∈Z
得kπ![]() x≤kπ
x≤kπ![]() ,k∈Z
,k∈Z
即函数的增区间为[kπ![]() ,kπ
,kπ![]() ],k∈Z,
],k∈Z,
∵x∈(0,π),
∴当k=0时,![]() x
x![]() ,此时0<x
,此时0<x![]() ,
,
当k=1时,![]() x≤π
x≤π![]() ,此时
,此时![]() x<π,
x<π,
综上函数的递增区间为(0,![]() ],[
],[![]() ,π).
,π).
(2)若f(x0)![]() ,
,
则2sin(2x0![]() )﹣1
)﹣1![]() ,
,
则sin(2x0![]() )
)![]() ,
,
∵x0∈[![]() ,
,![]() ],∴2x0∈[
],∴2x0∈[![]() ,π],
,π],
2x0![]() ∈[
∈[![]() ,
,![]() ],则cos(2x0
],则cos(2x0![]() )
)![]() ,
,
则cos2x0=cos(2x0![]() )=cos(2x0
)=cos(2x0![]() )cos
)cos![]() sin(2x0
sin(2x0![]() )sin
)sin![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初始溶液含杂质2%,每过滤一次可使杂质含量减少
 .
.(1)写出杂质含量y与过滤次数n的函数关系式;
(2)过滤7次后的杂质含量是多少?过滤8次后的杂质含量是多少?至少应过滤几次才能使产品达到市场要求?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的最大值为
的最大值为 .
.(1)若关于
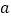 的方程
的方程 的两个实数根为
的两个实数根为 ,求证:
,求证: ;
;(2)当
 时,证明函数
时,证明函数 在函数
在函数 的最小零点
的最小零点 处取得极小值.
处取得极小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
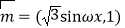 ,
,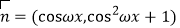 ,设函数
,设函数 .
.(1)若函数
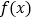 的图象关于直线
的图象关于直线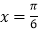 对称,且
对称,且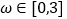 时,求函数
时,求函数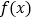 的单调增区间;
的单调增区间;(2)在(1)的条件下,当
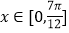 时,函数
时,函数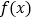 有且只有一个零点,求实数
有且只有一个零点,求实数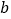 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
 .
.(Ⅰ)求
 的最小值及取得最小值时
的最小值及取得最小值时 的取值范围;
的取值范围;(Ⅱ)若集合
 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=asinωx+bcosωx(ω>0)的定义域为R,最小正周期为π,且对任意实数x,恒有
 成立.
成立.
(1)求实数a和b的值;
(2)作出函数f(x)在区间(0,π)上的大致图象;
(3)若两相异实数x1、x2∈(0,π),且满足f(x1)=f(x2),求f(x1+x2)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.向量
 与
与 是共线向量,则A,B,C,D必在同一直线上
是共线向量,则A,B,C,D必在同一直线上B.向量
 与
与 平行,则
平行,则 与
与 的方向相同或相反
的方向相同或相反C.向量
 与向量
与向量 是平行向量
是平行向量D.单位向量都相等
相关试题

