【题目】已知函数![]() 的最大值为
的最大值为![]() .
.
(1)若关于![]() 的方程
的方程![]() 的两个实数根为
的两个实数根为![]() ,求证:
,求证:![]() ;
;
(2)当![]() 时,证明函数
时,证明函数![]() 在函数
在函数![]() 的最小零点
的最小零点![]() 处取得极小值.
处取得极小值.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】分析:(1)本小问的解决方法是利用![]() 这个条件,得到含有
这个条件,得到含有![]() 的等式,对等式进行变形处理,使得等式左边是
的等式,对等式进行变形处理,使得等式左边是![]() ,右边是分式
,右边是分式![]() 。则求证目标不等式等价于证等式右端的部分
。则求证目标不等式等价于证等式右端的部分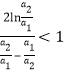 ,运用作差比较法构造函数
,运用作差比较法构造函数![]() ,对
,对![]() 运用导数进行研究,即可证明原不等式;
运用导数进行研究,即可证明原不等式;
(3)讨论函数的单调性,取绝对值得到![]() 的分段形式,若证明
的分段形式,若证明![]() ,则证明
,则证明![]() ,记
,记![]() ,求导分析单调性即可证得.
,求导分析单调性即可证得.
详解:(1)![]() ,由
,由![]() ,
,
得![]() ;由
;由![]() ,得
,得![]() ;
;
所以,![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,
,
所以![]() ,
,
不妨设![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴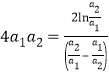 ,
,
设![]() ,则
,则![]() ,
,
所以,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,则
,则![]() ,
,
因![]() ,故
,故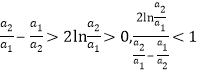 ,所以
,所以![]() ;
;
(2)由(1)可知,![]() 在区间
在区间![]() 单调递增,又
单调递增,又![]() 时,
时,![]() ,
,
易知,![]() 在
在![]() 递增,
递增,![]() ,
,
∴![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
当![]() 时,
时,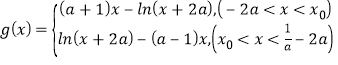 ,
,
于是![]() 时,
时,![]() ,
,
所以,若证明![]() ,则证明
,则证明![]() ,
,
记![]() ,
,
则![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 内单调递增,∴
内单调递增,∴![]() ,
,
∵![]() ,
,
∴![]() 在
在![]() 内单调递增,
内单调递增,
∴![]() ,
,
于是![]() 时,
时,![]() .
.
所以![]() 在
在![]() 递减.
递减.
当![]() 时,相应的
时,相应的![]() .
.
所以![]() 在
在![]() 递增.
递增.
故![]() 是
是![]() 的极小值点.
的极小值点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的一个焦点为
的一个焦点为 ,离心率为
,离心率为 .不过原点的直线
.不过原点的直线 与椭圆
与椭圆 相交于
相交于 两点,设直线
两点,设直线 ,直线
,直线 ,直线
,直线 的斜率分别为
的斜率分别为 ,且
,且 成等比数列.
成等比数列.(1)求
 的值;
的值;(2)若点
 在椭圆
在椭圆 上,满足
上,满足 的直线
的直线 是否存在?若存在,求出直线
是否存在?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,点
,点 为椭圆上一点.
为椭圆上一点. (1)求椭圆C的方程;
(2)已知两条互相垂直的直线
 ,
, 经过椭圆
经过椭圆 的右焦点
的右焦点 ,与椭圆
,与椭圆 交于
交于 四点,求四边形
四点,求四边形 面积的的取值范围.
面积的的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初始溶液含杂质2%,每过滤一次可使杂质含量减少
 .
.(1)写出杂质含量y与过滤次数n的函数关系式;
(2)过滤7次后的杂质含量是多少?过滤8次后的杂质含量是多少?至少应过滤几次才能使产品达到市场要求?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
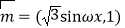 ,
,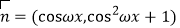 ,设函数
,设函数 .
.(1)若函数
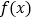 的图象关于直线
的图象关于直线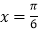 对称,且
对称,且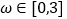 时,求函数
时,求函数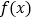 的单调增区间;
的单调增区间;(2)在(1)的条件下,当
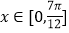 时,函数
时,函数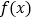 有且只有一个零点,求实数
有且只有一个零点,求实数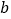 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=4cosωxsin(ωx
 )(ω>0)的最小正周期是π.
)(ω>0)的最小正周期是π.(1)求函数f(x)在区间(0,π)上的单调递增区间;
(2)若f(x0)
 ,x0∈[
,x0∈[ ,
, ],求cos2x0的值.
],求cos2x0的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
 .
.(Ⅰ)求
 的最小值及取得最小值时
的最小值及取得最小值时 的取值范围;
的取值范围;(Ⅱ)若集合
 ,求实数
,求实数 的取值范围.
的取值范围.
相关试题

