【题目】设函数f(x)=asinωx+bcosωx(ω>0)的定义域为R,最小正周期为π,且对任意实数x,恒有![]() 成立.
成立.

(1)求实数a和b的值;
(2)作出函数f(x)在区间(0,π)上的大致图象;
(3)若两相异实数x1、x2∈(0,π),且满足f(x1)=f(x2),求f(x1+x2)的值.
参考答案:
【答案】(1)a=2,b=2![]() .(2)见解析 (3)f(x1+x2)=2
.(2)见解析 (3)f(x1+x2)=2![]() .
.
【解析】
(1)将f(x)=asinωx+bcosωx化为f(x)![]() sin(ωx+φ),由题意可得
sin(ωx+φ),由题意可得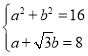 ,从而可求得a和b的值;
,从而可求得a和b的值;
(2)由f(x)=4sin(2x![]() )利用五点作图法即可作出其大致图象;
)利用五点作图法即可作出其大致图象;
(3)当0<x1<x2![]() 时,x1+x2
时,x1+x2![]() ,当
,当![]() x1<x2<π时,x1+x2
x1<x2<π时,x1+x2![]() ,从而可求得f(x1+x2)的值.
,从而可求得f(x1+x2)的值.
解(1)∵f(x)=asinωx+bcosωx![]() sin(ωx+φ)(ω>0),
sin(ωx+φ)(ω>0),
又f(x)≤f(![]() )=4恒成立,
)=4恒成立,
∴![]() 4,即a2+b2=16.…①
4,即a2+b2=16.…①
∵f(x)的最小正周期为π,
∴ω![]() 2,
2,
即f(x)=asin2x+bcos2x(ω>0).
又f(x)max=f(![]() )=4,
)=4,
∴asin![]() bcos
bcos![]() 4,
4,
即a![]() b=8.…②
b=8.…②
由①、②解得a=2,b=2![]() .
.
(2)由(1)知f(x)=2sin2x+2![]() cos2x=4sin(2x
cos2x=4sin(2x![]() ).
).
∵0<x<π,
∴![]() 2x
2x![]() ,列表如下:
,列表如下:
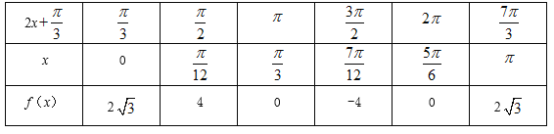
∴函数f(x)的图象如图所示:
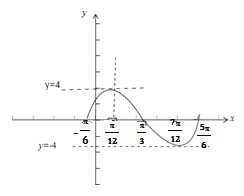
(3)∵f(x1)=f(x2),由f(x)=4sin(2x![]() )知,f(0)=f(
)知,f(0)=f(![]() )=2
)=2![]() ,
,
如图:
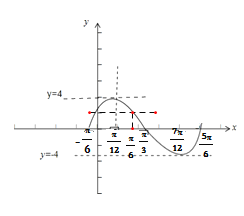
∴当0<x1<x2![]() 时,x1+x2=2
时,x1+x2=2![]() ,
,
∴f(x1+x2)=f(![]() )=4
)=4![]() 2
2![]() ;
;
当![]() x1<x2<π时,x1+x2=2
x1<x2<π时,x1+x2=2![]() ,
,
∴f(x1+x2)=f(![]() )=4sin
)=4sin![]() 2
2![]()
综上,f(x1+x2)=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
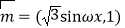 ,
,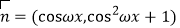 ,设函数
,设函数 .
.(1)若函数
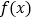 的图象关于直线
的图象关于直线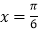 对称,且
对称,且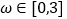 时,求函数
时,求函数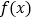 的单调增区间;
的单调增区间;(2)在(1)的条件下,当
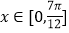 时,函数
时,函数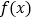 有且只有一个零点,求实数
有且只有一个零点,求实数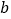 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=4cosωxsin(ωx
 )(ω>0)的最小正周期是π.
)(ω>0)的最小正周期是π.(1)求函数f(x)在区间(0,π)上的单调递增区间;
(2)若f(x0)
 ,x0∈[
,x0∈[ ,
, ],求cos2x0的值.
],求cos2x0的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
 .
.(Ⅰ)求
 的最小值及取得最小值时
的最小值及取得最小值时 的取值范围;
的取值范围;(Ⅱ)若集合
 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.向量
 与
与 是共线向量,则A,B,C,D必在同一直线上
是共线向量,则A,B,C,D必在同一直线上B.向量
 与
与 平行,则
平行,则 与
与 的方向相同或相反
的方向相同或相反C.向量
 与向量
与向量 是平行向量
是平行向量D.单位向量都相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列结论是否正确(正确的在括号内打“√”,错误的打“×”),并说明理由.
(1)若
 与
与 都是单位向量,则
都是单位向量,则 .( )
.( )(2)方向为南偏西60°的向量与北偏东60°的向量是共线向量.( )
(3)直角坐标平面上的x轴、y轴都是向量.( )
(4)若
 与
与 是平行向量,则
是平行向量,则 .( )
.( )(5)若用有向线段表示的向量
 与
与 不相等,则点M与N不重合.( )
不相等,则点M与N不重合.( )(6)海拔、温度、角度都不是向量.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)的定义域为D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明你的结论;
(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.
相关试题

