【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() :
: ![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() :
: ![]() .
.
(1)将曲线![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 、2倍后得到曲线
、2倍后得到曲线![]() ,求
,求![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
参考答案:
【答案】(1)![]() ,
, ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据![]() 将直线极坐标方程化为直角坐标方程
将直线极坐标方程化为直角坐标方程![]() ,根据图像伸缩变换得曲线
,根据图像伸缩变换得曲线![]() 的直角坐标方程
的直角坐标方程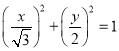 ,再根据椭圆参数方程得曲线
,再根据椭圆参数方程得曲线![]() 的参数方程
的参数方程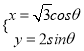 (
(![]() 为参数)(2)根据点到直线距离公式得点
为参数)(2)根据点到直线距离公式得点![]() 到直线
到直线![]() 的距离为
的距离为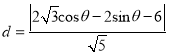
利用配角公式得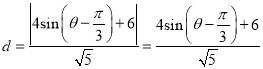 ,再根据正弦函数性质得最值及对应自变量的取值
,再根据正弦函数性质得最值及对应自变量的取值
试题解析:(1)由题意知,直线![]() 的直角坐标方程为:
的直角坐标方程为: ![]() ,
,
∵曲线![]() 的直角坐标方程为:
的直角坐标方程为: 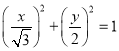 ,
,
∴曲线![]() 的参数方程为:
的参数方程为: 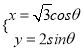 (
(![]() 为参数)
为参数)
(2)设点![]() 的坐标
的坐标![]() ,则点
,则点![]() 到直线
到直线![]() 的距离为:
的距离为:
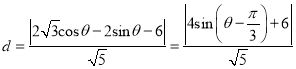 ,
,
∴当![]() 时,点
时,点![]() ,此时
,此时![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
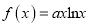 图象上点
图象上点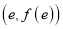 处的切线方程与直线
处的切线方程与直线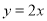 平行(其中
平行(其中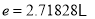 ),
),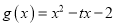 .
.(Ⅰ)求函数
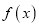 的解析式;
的解析式;(Ⅱ)求函数
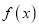 在
在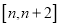 (
(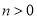 )上的最小值;
)上的最小值;(Ⅲ)对一切
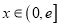 ,
, 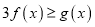 恒成立,求实数
恒成立,求实数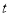 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
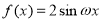 (
(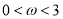 )在
)在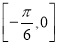 上的最小值为
上的最小值为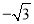 ,当把
,当把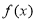 的图象上所有的点向右平移
的图象上所有的点向右平移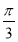 个单位后,得到函数
个单位后,得到函数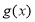 的图象.
的图象.(1)求函数
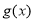 的解析式;
的解析式;(2)在△
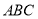 中,角
中,角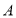 ,
,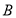 ,
,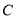 对应的边分别是
对应的边分别是 ,
,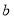 ,
,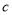 ,若函数
,若函数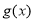 在
在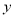 轴右侧的第一个零点恰为
轴右侧的第一个零点恰为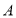 ,
,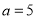 ,求△
,求△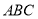 的面积
的面积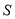 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
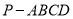 的底面
的底面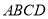 是正方形,侧棱
是正方形,侧棱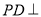 底面
底面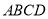 ,
, 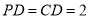 ,
, 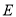 是
是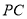 的中点.
的中点.(1)求二面角
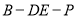 的平面角的余弦值;
的平面角的余弦值;(2)在被
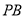 上是否存在点
上是否存在点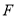 ,使
,使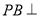 平面
平面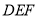 ?证明你的结论.
?证明你的结论.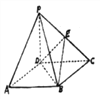
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为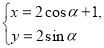 (
(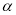 为参数).以平面直角坐标系的原点
为参数).以平面直角坐标系的原点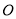 为极点,
为极点,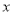 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线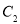 的极坐标方程为
的极坐标方程为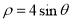 .
.(1)求曲线
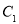 的普通方程和曲线
的普通方程和曲线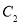 的直角坐标方程;
的直角坐标方程;(2)求曲线
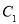 和
和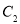 公共弦的长度.
公共弦的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cos xsin 2x,下列结论中正确的是________(填入正确结论的序号).
①y=f(x)的图象关于点(2π,0)中心对称;
②y=f(x)的图象关于直线x=π对称;
③f(x)的最大值为
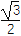 ;
;④f(x)既是奇函数,又是周期函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有3名男生,4名女生,在下列不同要求下,求不同的排列方法种数:
(1)选其中5人排成一排
(2)全体排成一排,甲不站在排头也不站在排尾
(3)全体排成一排,男生互不相邻
(4)全体排成一排,甲、乙两人中间恰好有3人
相关试题

