【题目】有3名男生,4名女生,在下列不同要求下,求不同的排列方法种数:
(1)选其中5人排成一排
(2)全体排成一排,甲不站在排头也不站在排尾
(3)全体排成一排,男生互不相邻
(4)全体排成一排,甲、乙两人中间恰好有3人
参考答案:
【答案】(1)2520;(2)3600;(3)1440;(4)720.
【解析】试题分析:
(1)属于从7个不同元素中任选5个的排列;
(2)第一步先安排特殊元素甲,第二步其他6人全排列即可;
(3)第一步排所有女生,第二步在5个空位(含两端)排3个男生;
(4)第一步选3人排在甲乙中间(注意这3人全排列),第二步甲乙两也全排列,第三步甲乙和他们中间的3人作为一个整体与剩下的2人变成3个元素再全排列.
试题解析:
(1)![]() =2520(种).
=2520(种).
(2)先排甲,有5种方法,其余6人有![]() 种方法,故共有5×
种方法,故共有5×![]() =3600(种).
=3600(种).
(3)男生不相邻,而女生不作要求,∴应先排女生,有![]() 种方法,
种方法,
再在女生之间及首尾空出的5个空位中任选3个空位排男生,有![]() 种方法,故共有
种方法,故共有![]() ·
·![]() =1440(种).
=1440(种).
(4)把甲、乙及中间3人看作一个整体,
第一步先排甲、乙两人有![]() 种方法,
种方法,
再从剩下的5人中选3人排到中间,有![]() 种方法,
种方法,
最后把甲、乙及中间3人看作一个整体,与剩余2人排列,有![]() 种方法,
种方法,
故共有![]() ·
·![]() ·
·![]() =720(种).
=720(种).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
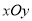 中,已知曲线
中,已知曲线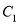 :
: 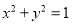 ,以平面直角坐标系
,以平面直角坐标系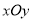 的原点
的原点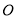 为极点,
为极点, 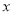 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线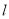 :
: 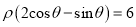 .
.(1)将曲线
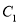 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的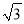 、2倍后得到曲线
、2倍后得到曲线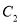 ,求
,求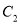 的参数方程;
的参数方程;(2)在曲线
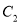 上求一点
上求一点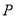 ,使点
,使点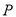 到直线
到直线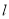 的距离最大,并求出此最大值.
的距离最大,并求出此最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
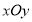 中,曲线
中,曲线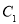 的参数方程为
的参数方程为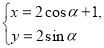 (
(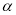 为参数).以平面直角坐标系的原点
为参数).以平面直角坐标系的原点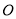 为极点,
为极点,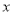 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线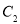 的极坐标方程为
的极坐标方程为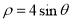 .
.(1)求曲线
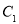 的普通方程和曲线
的普通方程和曲线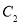 的直角坐标方程;
的直角坐标方程;(2)求曲线
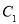 和
和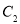 公共弦的长度.
公共弦的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cos xsin 2x,下列结论中正确的是________(填入正确结论的序号).
①y=f(x)的图象关于点(2π,0)中心对称;
②y=f(x)的图象关于直线x=π对称;
③f(x)的最大值为
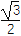 ;
;④f(x)既是奇函数,又是周期函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出
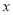 与销售额
与销售额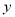 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据: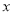
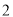
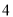
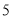
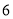
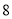
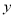
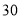
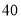
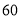
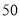
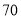
(1)求回归直线方程;
(2)试预测广告费支出为
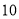 万元时,销售额多大?
万元时,销售额多大?(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过
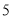 的概率.(参考数据:
的概率.(参考数据: 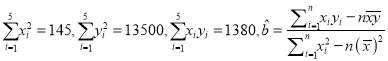 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=
 ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积 -
科目: 来源: 题型:
查看答案和解析>>【题目】一盒中放有的黑球和白球,其中黑球4个,白球5个.
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率.
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
(3)从盒中不放回的每次摸一球,若取到白球则停止摸球,求取到第三次时停止摸球的概率
相关试题

