【题目】已知函数![]() 图象上点
图象上点![]() 处的切线方程与直线
处的切线方程与直线![]() 平行(其中
平行(其中![]() ),
),![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求函数![]() 在
在![]() (
(![]() )上的最小值;
)上的最小值;
(Ⅲ)对一切![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)  ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】试题分析:(I)根据切线方程与直线![]() 平行得到切线的斜率为2,即可得到
平行得到切线的斜率为2,即可得到![]() ,求出函数的导函数把
,求出函数的导函数把![]() 代入即可求出
代入即可求出![]() 的值得到函数的解析式;(II)令
的值得到函数的解析式;(II)令![]() 求出
求出![]() 的值为
的值为![]() ,由函数定义域
,由函数定义域![]() ,所以在
,所以在![]() 和
和![]() 上讨论函数的增减性,分两种情况:当
上讨论函数的增减性,分两种情况:当![]() 属于
属于![]() 得到函数的最小值为
得到函数的最小值为![]() ;当
;当![]() 时,根据函数为单调增得到函数的最小值为
时,根据函数为单调增得到函数的最小值为![]() ,求出值即可;(III)把
,求出值即可;(III)把![]() 的解析式代入不等式
的解析式代入不等式![]() 中解出
中解出![]() ,然后令
,然后令![]() ,求出
,求出![]() 时
时![]() 的值,然后在定义域
的值,然后在定义域![]() 上分区间讨论函数的增减性,求出
上分区间讨论函数的增减性,求出![]() 的最大值,
的最大值, ![]() 要大于等于
要大于等于![]() 的最大值即为不等数恒成立,即可求出
的最大值即为不等数恒成立,即可求出![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)由点![]() 处的切线方程为直线
处的切线方程为直线![]() 平行,
平行,
得该切线斜率为2,即![]() .
.
又![]() ,令
,令![]() ,
, ![]() ,所以
,所以![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,显然
,显然![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以函数![]() 在
在![]() 上单调递减.当
上单调递减.当![]() 时,
时, ![]() ,
,
所以函数![]() 在
在![]() 上单调递增.
上单调递增.
①![]() 时,
时, ![]()
![]() ;
;
②![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
因此![]()
![]() ;
;
所以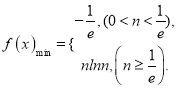
(Ⅲ)对一切![]() ,
, ![]() 恒成立,
恒成立,
又![]() ,
, ![]() ,
,
即![]() .
.
设![]() ,
, ![]() .
.
则![]()
![]()
![]() ,
,
由![]() 得
得![]() 或
或![]() ,
, ![]() ,
, ![]() ,
, ![]() 单调递增,
单调递增,
![]() ,
, ![]() ,
, ![]() 单调递减,
单调递减, ![]() ,
, ![]() ,
, ![]() 单调递增,
单调递增,
![]() ,且
,且![]()
![]() ,
,
所以![]() .
.
因为对一切![]() ,
, ![]() 恒成立,
恒成立,
![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
(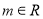 ),
),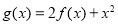 ,
,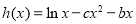 .
.(1)求函数
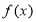 的单调区间;
的单调区间;(2)当
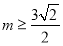 时,
时,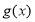 的两个极值点为
的两个极值点为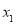 ,
, (
(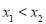 ).
).①证明:
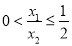 ;
;②若
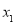 ,
,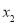 恰为
恰为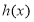 的零点,求
的零点,求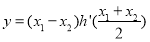 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
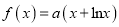 (
(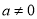 ),
),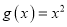 .
.(1)若
 的图象在
的图象在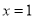 处的切线恰好也是
处的切线恰好也是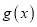 图象的切线.
图象的切线.①求实数
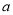 的值;
的值;②若方程
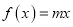 在区间
在区间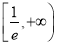 内有唯一实数解,求实数
内有唯一实数解,求实数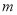 的取值范围.
的取值范围.(2)当
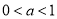 时,求证:对于区间
时,求证:对于区间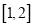 上的任意两个不相等的实数
上的任意两个不相等的实数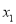 ,
, 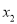 ,都有
,都有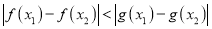 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
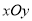 中,以原点
中,以原点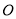 为极点,以
为极点,以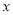 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线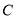 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;(2)设
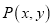 是曲线
是曲线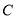 上的动点,求
上的动点,求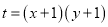 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
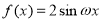 (
(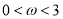 )在
)在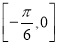 上的最小值为
上的最小值为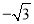 ,当把
,当把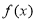 的图象上所有的点向右平移
的图象上所有的点向右平移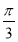 个单位后,得到函数
个单位后,得到函数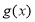 的图象.
的图象.(1)求函数
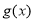 的解析式;
的解析式;(2)在△
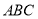 中,角
中,角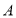 ,
,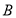 ,
,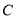 对应的边分别是
对应的边分别是 ,
,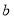 ,
,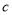 ,若函数
,若函数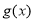 在
在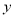 轴右侧的第一个零点恰为
轴右侧的第一个零点恰为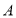 ,
,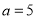 ,求△
,求△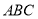 的面积
的面积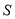 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
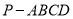 的底面
的底面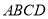 是正方形,侧棱
是正方形,侧棱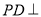 底面
底面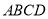 ,
, 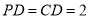 ,
, 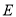 是
是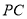 的中点.
的中点.(1)求二面角
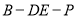 的平面角的余弦值;
的平面角的余弦值;(2)在被
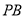 上是否存在点
上是否存在点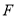 ,使
,使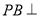 平面
平面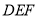 ?证明你的结论.
?证明你的结论.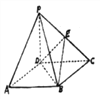
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
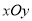 中,已知曲线
中,已知曲线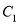 :
: 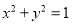 ,以平面直角坐标系
,以平面直角坐标系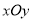 的原点
的原点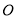 为极点,
为极点, 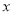 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线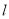 :
: 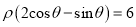 .
.(1)将曲线
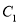 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的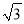 、2倍后得到曲线
、2倍后得到曲线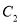 ,求
,求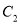 的参数方程;
的参数方程;(2)在曲线
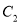 上求一点
上求一点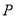 ,使点
,使点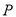 到直线
到直线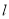 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
相关试题

