【题目】已知函数f(x)=cos xsin 2x,下列结论中正确的是________(填入正确结论的序号).
①y=f(x)的图象关于点(2π,0)中心对称;
②y=f(x)的图象关于直线x=π对称;
③f(x)的最大值为![]() ;
;
④f(x)既是奇函数,又是周期函数.
参考答案:
【答案】①④
【解析】依题意,对于①,f(4π-x)=cos(4π-x)·sin[2(4π-x)]=-cos x·sin 2x=-f(x),因此函数y=f(x)的图象关于点(2π,0)中心对称,①正确;对于②,f![]() =
=![]() ,f
,f![]() =-
=-![]() ,因此f
,因此f![]() ≠f
≠f![]() ,函数y=f(x)的图象不关于直线x=π对称,②不正确;对于③,f(x)=2sin xcos2x=2(sin x-sin3x);令t=sin x,则y=2(t-t3),t∈[-1,1],y′=2(1-3t2),当-
,函数y=f(x)的图象不关于直线x=π对称,②不正确;对于③,f(x)=2sin xcos2x=2(sin x-sin3x);令t=sin x,则y=2(t-t3),t∈[-1,1],y′=2(1-3t2),当-![]() <t<
<t<![]() 时,y′>0;当-1≤t<-
时,y′>0;当-1≤t<-![]() 或
或![]() <t≤1时,y′<0,因此函数y=2(t-t3)在[-1,1]上的最大值是y=2
<t≤1时,y′<0,因此函数y=2(t-t3)在[-1,1]上的最大值是y=2![]() =
=![]() ,即函数f(x)的最大值是
,即函数f(x)的最大值是![]() ,③不正确;对于④,f(-x)=-f(x),且f(2π+x)=2sin(2π+x)cos2(2π+x)=2sin xcos2x=f(x),因此函数f(x)既是奇函数,又是周期函数,④正确.综上所述,其中正确的结论是①④.
,③不正确;对于④,f(-x)=-f(x),且f(2π+x)=2sin(2π+x)cos2(2π+x)=2sin xcos2x=f(x),因此函数f(x)既是奇函数,又是周期函数,④正确.综上所述,其中正确的结论是①④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
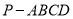 的底面
的底面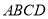 是正方形,侧棱
是正方形,侧棱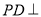 底面
底面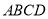 ,
, 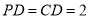 ,
, 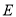 是
是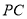 的中点.
的中点.(1)求二面角
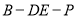 的平面角的余弦值;
的平面角的余弦值;(2)在被
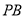 上是否存在点
上是否存在点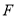 ,使
,使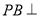 平面
平面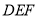 ?证明你的结论.
?证明你的结论.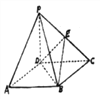
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
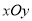 中,已知曲线
中,已知曲线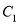 :
: 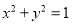 ,以平面直角坐标系
,以平面直角坐标系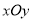 的原点
的原点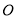 为极点,
为极点, 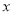 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线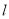 :
: 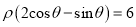 .
.(1)将曲线
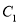 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的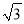 、2倍后得到曲线
、2倍后得到曲线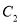 ,求
,求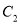 的参数方程;
的参数方程;(2)在曲线
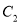 上求一点
上求一点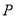 ,使点
,使点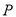 到直线
到直线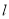 的距离最大,并求出此最大值.
的距离最大,并求出此最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
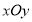 中,曲线
中,曲线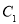 的参数方程为
的参数方程为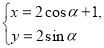 (
(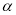 为参数).以平面直角坐标系的原点
为参数).以平面直角坐标系的原点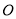 为极点,
为极点,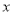 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线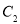 的极坐标方程为
的极坐标方程为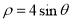 .
.(1)求曲线
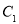 的普通方程和曲线
的普通方程和曲线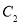 的直角坐标方程;
的直角坐标方程;(2)求曲线
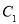 和
和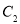 公共弦的长度.
公共弦的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】有3名男生,4名女生,在下列不同要求下,求不同的排列方法种数:
(1)选其中5人排成一排
(2)全体排成一排,甲不站在排头也不站在排尾
(3)全体排成一排,男生互不相邻
(4)全体排成一排,甲、乙两人中间恰好有3人
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出
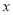 与销售额
与销售额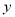 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据: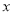
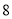
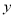
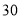
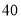
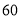
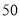
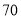
(1)求回归直线方程;
(2)试预测广告费支出为
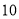 万元时,销售额多大?
万元时,销售额多大?(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过
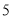 的概率.(参考数据:
的概率.(参考数据: 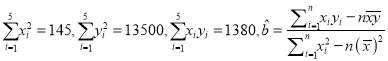 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=
 ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
相关试题

