【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;
(2)设![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)直接根据极坐标和直角坐标方程互化公式求解得到其直角坐标方程,然后,再将其化为标准方程即可判断其形状;(2)依据曲线![]() 的参数方程,可以设该点
的参数方程,可以设该点![]() 的三角形式,然后,借助于三角函数的有界性求最值.
的三角形式,然后,借助于三角函数的有界性求最值.
试题解析:(1)由ρ2-4![]() ρcos
ρcos![]() +7=0可得ρ2-4ρcosθ-4ρsinθ+7=0,化为直角坐标方程得x2+y2-4x-4y+7=0,即(x-2)2+(y-2)2=1,它表示以(2,2)为圆心,以1为半径的圆.
+7=0可得ρ2-4ρcosθ-4ρsinθ+7=0,化为直角坐标方程得x2+y2-4x-4y+7=0,即(x-2)2+(y-2)2=1,它表示以(2,2)为圆心,以1为半径的圆.
(2)由题意可设x=2+cosθ,y=2+sinθ,则t=(x+1)(y+1)=(3+cosθ)(3+sinθ)=9+3(sinθ+cosθ)+sinθcosθ.
令sinθ+cosθ=m,平方可得1+2sinθcosθ=m2,
所以sinθcosθ=![]() ,t=9+3m+
,t=9+3m+![]() =
=![]() m2+3m+
m2+3m+![]() (-
(-![]() ≤m≤
≤m≤![]() ).由二次函数的图象可知t的取值范围为
).由二次函数的图象可知t的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆
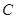
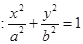 (
(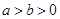 )的离心率是
)的离心率是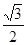 ,过点
,过点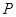 (
( ,
, )的动直线
)的动直线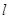 与椭圆相交于
与椭圆相交于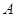 ,
,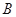 两点,当直线
两点,当直线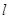 平行于
平行于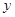 轴时,直线
轴时,直线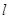 被椭圆
被椭圆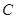 截得的线段长为
截得的线段长为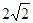 .
.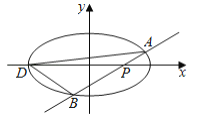
⑴求椭圆
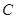 的方程:
的方程:⑵已知
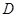 为椭圆的左端点,问: 是否存在直线
为椭圆的左端点,问: 是否存在直线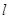 使得
使得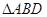 的面积为
的面积为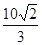 ?若不存在,说明理由,若存在,求出直线
?若不存在,说明理由,若存在,求出直线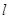 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
(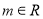 ),
),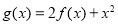 ,
,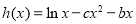 .
.(1)求函数
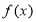 的单调区间;
的单调区间;(2)当
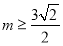 时,
时,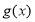 的两个极值点为
的两个极值点为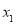 ,
, (
(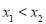 ).
).①证明:
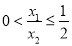 ;
;②若
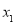 ,
,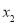 恰为
恰为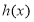 的零点,求
的零点,求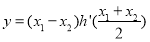 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
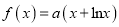 (
(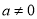 ),
),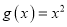 .
.(1)若
 的图象在
的图象在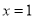 处的切线恰好也是
处的切线恰好也是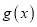 图象的切线.
图象的切线.①求实数
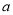 的值;
的值;②若方程
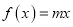 在区间
在区间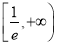 内有唯一实数解,求实数
内有唯一实数解,求实数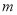 的取值范围.
的取值范围.(2)当
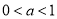 时,求证:对于区间
时,求证:对于区间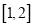 上的任意两个不相等的实数
上的任意两个不相等的实数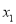 ,
, 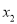 ,都有
,都有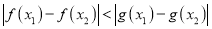 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
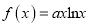 图象上点
图象上点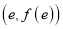 处的切线方程与直线
处的切线方程与直线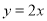 平行(其中
平行(其中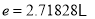 ),
),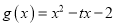 .
.(Ⅰ)求函数
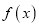 的解析式;
的解析式;(Ⅱ)求函数
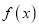 在
在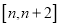 (
(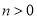 )上的最小值;
)上的最小值;(Ⅲ)对一切
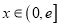 ,
, 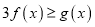 恒成立,求实数
恒成立,求实数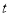 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
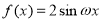 (
(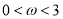 )在
)在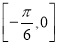 上的最小值为
上的最小值为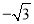 ,当把
,当把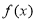 的图象上所有的点向右平移
的图象上所有的点向右平移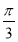 个单位后,得到函数
个单位后,得到函数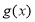 的图象.
的图象.(1)求函数
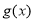 的解析式;
的解析式;(2)在△
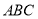 中,角
中,角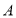 ,
,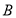 ,
,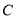 对应的边分别是
对应的边分别是 ,
,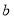 ,
,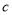 ,若函数
,若函数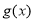 在
在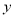 轴右侧的第一个零点恰为
轴右侧的第一个零点恰为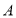 ,
,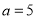 ,求△
,求△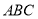 的面积
的面积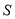 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
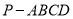 的底面
的底面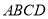 是正方形,侧棱
是正方形,侧棱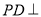 底面
底面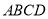 ,
, 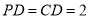 ,
, 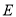 是
是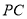 的中点.
的中点.(1)求二面角
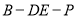 的平面角的余弦值;
的平面角的余弦值;(2)在被
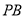 上是否存在点
上是否存在点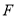 ,使
,使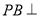 平面
平面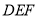 ?证明你的结论.
?证明你的结论.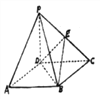
相关试题

