【题目】如图,椭圆![]()
![]() (
(![]() )的离心率是
)的离心率是![]() ,过点
,过点![]() (
(![]() ,
,![]() )的动直线
)的动直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
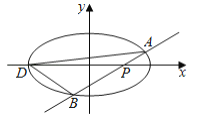
⑴求椭圆![]() 的方程:
的方程:
⑵已知![]() 为椭圆的左端点,问: 是否存在直线
为椭圆的左端点,问: 是否存在直线![]() 使得
使得![]() 的面积为
的面积为![]() ?若不存在,说明理由,若存在,求出直线
?若不存在,说明理由,若存在,求出直线![]() 的方程.
的方程.
参考答案:
【答案】(1)![]() ;(2)存在直线
;(2)存在直线![]() 方程
方程![]() 使得
使得![]() .
.
【解析】试题分析:(1)借助题设条件建立方程组求解;(2)依据题设运用直线与椭圆的位置关系进行探求.
试题解析:
(1)![]() 椭圆
椭圆![]() :
:![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,
两点,
当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() ,
,
![]() 点
点![]() 在椭圆
在椭圆![]() 上,
上,
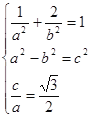 ,解得:
,解得:![]() ,………………4分
,………………4分
![]() 椭圆的方程为
椭圆的方程为![]() ………………………5分,
………………………5分,
(2)当直线![]() 与
与![]() 轴平行时,
轴平行时,![]() 不存在,…………………6分,
不存在,…………………6分,
![]() 设直线
设直线![]() 的方程为
的方程为![]() ,并设两点
,并设两点![]() ,
,![]() ,
,
联立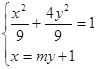 ,得
,得![]() ,
,
其判别式![]() ,…………8分,
,…………8分,
![]() ,
,![]() ,
,
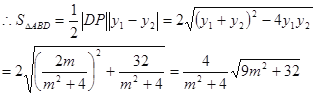 ,…………10分
,…………10分
假设存在直线![]() ,则有
,则有![]() ,
,
解得![]() ,负解删除,
,负解删除,![]() ,……………………12分
,……………………12分
故存在直线![]() 方程
方程![]() 使得
使得![]() …………13分.
…………13分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
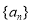 满足:
满足: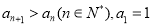 ,该数列的前三项分别加上1,1,3后成等比数列,且
,该数列的前三项分别加上1,1,3后成等比数列,且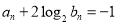 .
.(1)求数列
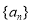 ,
,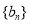 的通项公式;
的通项公式;(2)求数列
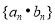 的前
的前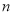 项和
项和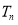 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
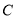 :
:  的离心率为
的离心率为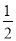 ,且过点
,且过点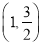 .若点
.若点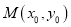 在椭圆
在椭圆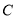 上,则点
上,则点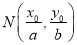 称为点
称为点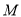 的一个“椭点”.
的一个“椭点”.(1)求椭圆
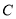 的标准方程;
的标准方程;(2)若直线
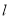 :
: 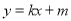 与椭圆
与椭圆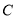 相交于
相交于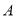 ,
, 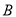 两点,且
两点,且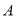 ,
, 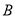 两点的“椭点”分别为
两点的“椭点”分别为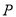 ,
, 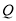 ,以
,以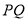 为直径的圆经过坐标原点,试求
为直径的圆经过坐标原点,试求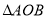 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个结论:
(1)如果
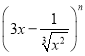 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中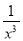 的系数是-21;
的系数是-21;(2)用相关指数
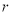 来刻画回归效果,
来刻画回归效果, 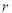 的值越大,说明模型的拟合效果越差;
的值越大,说明模型的拟合效果越差;(3)若
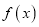 是
是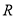 上的奇函数,且满足
上的奇函数,且满足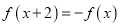 ,则
,则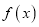 的图象关于
的图象关于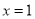 对称;
对称;(4)一个篮球运动员投篮一次得3分的概率为
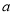 ,得2分的概率为
,得2分的概率为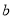 ,不得分的概率为
,不得分的概率为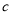 ,且
,且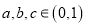 ,已知他投篮一次得分的数学期望为2,则
,已知他投篮一次得分的数学期望为2,则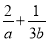 的最小值为
的最小值为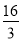 ;
;其中正确结论的序号为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
(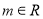 ),
),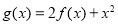 ,
,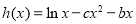 .
.(1)求函数
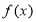 的单调区间;
的单调区间;(2)当
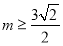 时,
时,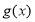 的两个极值点为
的两个极值点为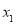 ,
, (
(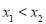 ).
).①证明:
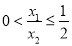 ;
;②若
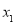 ,
,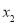 恰为
恰为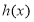 的零点,求
的零点,求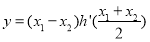 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
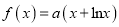 (
(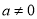 ),
),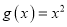 .
.(1)若
 的图象在
的图象在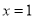 处的切线恰好也是
处的切线恰好也是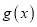 图象的切线.
图象的切线.①求实数
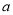 的值;
的值;②若方程
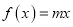 在区间
在区间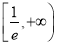 内有唯一实数解,求实数
内有唯一实数解,求实数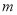 的取值范围.
的取值范围.(2)当
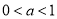 时,求证:对于区间
时,求证:对于区间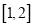 上的任意两个不相等的实数
上的任意两个不相等的实数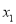 ,
, 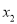 ,都有
,都有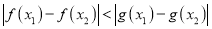 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
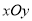 中,以原点
中,以原点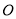 为极点,以
为极点,以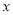 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线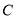 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;(2)设
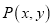 是曲线
是曲线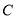 上的动点,求
上的动点,求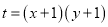 的取值范围.
的取值范围.
相关试题

