【题目】已知函数![]() (
(![]() ),
),![]() .
.
(1)若![]() 的图象在
的图象在![]() 处的切线恰好也是
处的切线恰好也是![]() 图象的切线.
图象的切线.
①求实数![]() 的值;
的值;
②若方程![]() 在区间
在区间![]() 内有唯一实数解,求实数
内有唯一实数解,求实数![]() 的取值范围.
的取值范围.
(2)当![]() 时,求证:对于区间
时,求证:对于区间![]() 上的任意两个不相等的实数
上的任意两个不相等的实数![]() ,
, ![]() ,都有
,都有![]() 成立.
成立.
参考答案:
【答案】(1)①![]() ,
, ![]() ;(2)详见解析
;(2)详见解析
【解析】试题分析:(1)①首先求函数![]() 的图象在
的图象在![]() 处的切线,
处的切线, ![]() ,
, ![]() ,又因为切点为
,又因为切点为![]() ,所以切线方程为
,所以切线方程为![]() ,于是问题转化为直线
,于是问题转化为直线![]() 与函数
与函数![]() 图象相切,于是可以根据直线与抛物线相切进行解题;②问题转化为方程
图象相切,于是可以根据直线与抛物线相切进行解题;②问题转化为方程![]() 在区间
在区间![]() 内有唯一实数解,参变量分离得
内有唯一实数解,参变量分离得![]() ,设
,设![]() ,
, ![]() ,研究
,研究![]() 的单调性、极值,转化为直线
的单调性、极值,转化为直线![]() 与
与![]() 有且只有一个交点,(2)当
有且只有一个交点,(2)当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增, ![]() 在
在![]() 上单调递增,设
上单调递增,设![]() ,则
,则![]() ,
, ![]() ,于是问题转化为
,于是问题转化为![]() ,构造函数
,构造函数![]() ,通过函数
,通过函数![]() 在
在![]() 上单调递减,可以求出
上单调递减,可以求出![]() 的取值范围.
的取值范围.
试题解析:①![]() ,∴
,∴![]() ,
, ![]() ,切点为
,切点为![]() ,
,
∴切线方程为![]() ,即
,即![]() ,
,
联立![]() ,消去
,消去![]() ,可得
,可得![]() ,
, ![]() ,
,
∴![]() ;
;
②由![]() ,得
,得![]() ,
,
设![]() ,
, ![]() ,则问题等价于
,则问题等价于![]() 与
与![]() 的图象在
的图象在![]() 上有唯一交点,
上有唯一交点,
∵![]() ,∴
,∴![]() ,
, ![]() ,函数单调递增,
,函数单调递增, ![]() ,
, ![]() ,函数单调递减,
,函数单调递减,
∵![]() ,
, ![]() ,且
,且![]() 时,
时, ![]() ,
,
∴![]() ;
;
证明:(2)不妨设![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() 可化为
可化为![]()
∴![]()
设![]() ,即
,即![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() 恒成立,即
恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
∵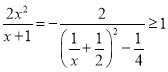 ,∴
,∴![]() ,
,
从而,当![]() 时,命题成立.
时,命题成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个结论:
(1)如果
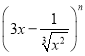 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中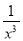 的系数是-21;
的系数是-21;(2)用相关指数
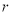 来刻画回归效果,
来刻画回归效果, 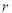 的值越大,说明模型的拟合效果越差;
的值越大,说明模型的拟合效果越差;(3)若
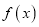 是
是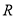 上的奇函数,且满足
上的奇函数,且满足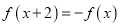 ,则
,则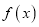 的图象关于
的图象关于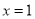 对称;
对称;(4)一个篮球运动员投篮一次得3分的概率为
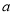 ,得2分的概率为
,得2分的概率为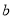 ,不得分的概率为
,不得分的概率为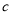 ,且
,且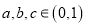 ,已知他投篮一次得分的数学期望为2,则
,已知他投篮一次得分的数学期望为2,则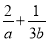 的最小值为
的最小值为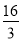 ;
;其中正确结论的序号为__________.
-
科目: 来源: 题型:
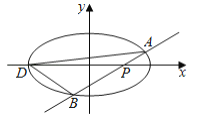
查看答案和解析>>【题目】如图,椭圆
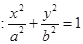 (
(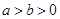 )的离心率是
)的离心率是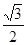 ,过点
,过点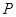 (
( ,
, )的动直线
)的动直线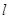 与椭圆相交于
与椭圆相交于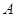 ,
,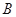 两点,当直线
两点,当直线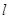 平行于
平行于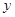 轴时,直线
轴时,直线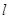 被椭圆
被椭圆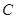 截得的线段长为
截得的线段长为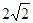 .
.
⑴求椭圆
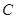 的方程:
的方程:⑵已知
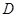 为椭圆的左端点,问: 是否存在直线
为椭圆的左端点,问: 是否存在直线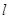 使得
使得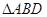 的面积为
的面积为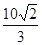 ?若不存在,说明理由,若存在,求出直线
?若不存在,说明理由,若存在,求出直线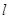 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
(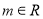 ),
),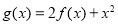 ,
,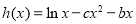 .
.(1)求函数
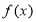 的单调区间;
的单调区间;(2)当
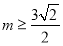 时,
时,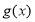 的两个极值点为
的两个极值点为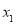 ,
, (
(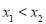 ).
).①证明:
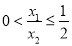 ;
;②若
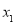 ,
,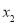 恰为
恰为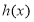 的零点,求
的零点,求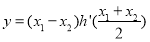 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
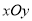 中,以原点
中,以原点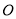 为极点,以
为极点,以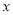 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线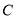 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;(2)设
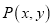 是曲线
是曲线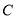 上的动点,求
上的动点,求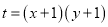 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
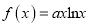 图象上点
图象上点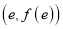 处的切线方程与直线
处的切线方程与直线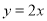 平行(其中
平行(其中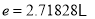 ),
),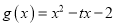 .
.(Ⅰ)求函数
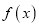 的解析式;
的解析式;(Ⅱ)求函数
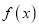 在
在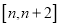 (
(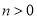 )上的最小值;
)上的最小值;(Ⅲ)对一切
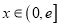 ,
, 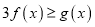 恒成立,求实数
恒成立,求实数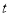 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
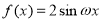 (
(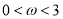 )在
)在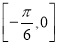 上的最小值为
上的最小值为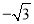 ,当把
,当把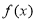 的图象上所有的点向右平移
的图象上所有的点向右平移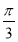 个单位后,得到函数
个单位后,得到函数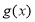 的图象.
的图象.(1)求函数
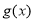 的解析式;
的解析式;(2)在△
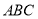 中,角
中,角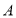 ,
,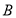 ,
,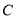 对应的边分别是
对应的边分别是 ,
,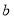 ,
,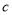 ,若函数
,若函数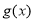 在
在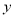 轴右侧的第一个零点恰为
轴右侧的第一个零点恰为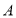 ,
,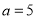 ,求△
,求△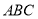 的面积
的面积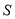 的最大值.
的最大值.
相关试题

