【题目】已知函数f(x)=![]() +x在x=1处的切线方程为2x﹣y+b=0.
+x在x=1处的切线方程为2x﹣y+b=0.
(Ⅰ)求实数a,b的值;
(Ⅱ)若函数g(x)=f(x)+![]() x2﹣kx,且g(x)是其定义域上的增函数,求实数k的取值范围.
x2﹣kx,且g(x)是其定义域上的增函数,求实数k的取值范围.
参考答案:
【答案】(1) a=1,b=﹣1;(2) k≤3.
【解析】试题分析:(1)由切线方程,布列方程组,解之即可;(2)g(x)在其定义域(0,+∞)上是增函数,即g′(x)≥0在其定义域上恒成立,变量分离求最值即可.
试题解析:
(Ⅰ)∵f(x)=![]() +x,
+x,
∴f′(x)=![]() +1,
+1,
∵f(x)在x=1处的切线方程为2x﹣y+b=0,
∴![]() +1=2, 2﹣1+b=0, ∴a=1,b=﹣1;
+1=2, 2﹣1+b=0, ∴a=1,b=﹣1;
(Ⅱ)f(x)=lnx+x,g(x)=![]() x2﹣kx+lnx+x,
x2﹣kx+lnx+x,
∴g′(x)=x﹣k+![]() +1,
+1,
∵g(x)在其定义域(0,+∞)上是增函数,∴g′(x)≥0在其定义域上恒成立,
∴x﹣k+![]() +1≥0在其定义域上恒成立 ∴k≤x+
+1≥0在其定义域上恒成立 ∴k≤x+![]() +1在其定义域上恒成立,
+1在其定义域上恒成立,
而x+![]() +1≥2
+1≥2![]() +1=3,当且仅当x=1时“=”成立, ∴k≤3.
+1=3,当且仅当x=1时“=”成立, ∴k≤3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=
 ﹣p
﹣p④回归直线一定过样本点的中心(
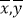 ).
).其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间20名工人年龄数据如下表:
年龄(岁)
19
24
26
30
34
35
40
合计
工人数(人)
1
3
3
5
4
3
1
20
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
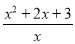 ,其中x∈[2,+∞).
,其中x∈[2,+∞).(1)求f(x)的最小值;
(2)若f(x)>a恒成立,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】轮船由甲地逆水匀速行驶至乙地,甲、乙两地相距s(km),水流速度为p(km/h),轮船在静水中的最大速度为q(km/h)(p,q为常数,且q>p),已知轮船每小时的燃料费用与轮船在静水中的速度v(km/h)成正比,比例系数为常数k.
(1)将全程燃料费用y(元)表示为静水中速度v(km/h)的函数;
(2)若s=100,p=10,q=110,k=2,为了使全程的燃料费用最少,轮船的实际行驶速度应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第x年与年产量f(x) 万件之间的关系如下表所示:
x
1
2
3
4
f(x)
4.00
5.58
7.00
8.44
若f(x)近似符合以下三种函数模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log
 x+a.
x+a.(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少30%,试根据所建立的函数模型,确定2015年的年产量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次函数f(x)=x2+(2t-1)x+1-2t.
(1)求证:对于任意t∈R,方程f(x)=1必有实数根;
(2)若
 <t<
<t< ,求证:方程f(x)=0在区间(-1,0)及
,求证:方程f(x)=0在区间(-1,0)及 内各有一个实数根.
内各有一个实数根.
相关试题

