【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第x年与年产量f(x) 万件之间的关系如下表所示:
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三种函数模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log![]() x+a.
x+a.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少30%,试根据所建立的函数模型,确定2015年的年产量.
参考答案:
【答案】(1) f(x)=![]() x+
x+![]() ,x∈N. (2) 9.1万件.
,x∈N. (2) 9.1万件.
【解析】试题分析:(1)分别代人不同模型,确定a,b值,再代人第三或四个量验证是否符合(2)先按模型计算2015年的年产量,再计算实际年产量.
试题解析:解:(1)符合条件的是f(x)=ax+b.
若模型为f(x)=2x+a,则由f(1)=21+a=4,得a=2,即f(x)=2x+2,
此时f(2)=6, f(3)=10, f(4)=18,与已知相差太大,不符合.
若模型为f(x)=log![]() x+a,则f(x)是减函数,与已知不符合.
x+a,则f(x)是减函数,与已知不符合.
由已知得![]() 解得
解得![]()
所以f(x)=![]() x+
x+![]() ,x∈N.
,x∈N.
(2)2015年预计年产量为f(7)=![]() ×7+
×7+![]() =13,2015年实际年产量为13×(1-30%)=9.1,
=13,2015年实际年产量为13×(1-30%)=9.1,
答:最适合的模型解析式为f(x)=![]() x+
x+![]() ,x∈N .2015年的实际产量为9.1万件.
,x∈N .2015年的实际产量为9.1万件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
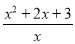 ,其中x∈[2,+∞).
,其中x∈[2,+∞).(1)求f(x)的最小值;
(2)若f(x)>a恒成立,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
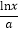 +x在x=1处的切线方程为2x﹣y+b=0.
+x在x=1处的切线方程为2x﹣y+b=0.(Ⅰ)求实数a,b的值;
(Ⅱ)若函数g(x)=f(x)+
 x2﹣kx,且g(x)是其定义域上的增函数,求实数k的取值范围.
x2﹣kx,且g(x)是其定义域上的增函数,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】轮船由甲地逆水匀速行驶至乙地,甲、乙两地相距s(km),水流速度为p(km/h),轮船在静水中的最大速度为q(km/h)(p,q为常数,且q>p),已知轮船每小时的燃料费用与轮船在静水中的速度v(km/h)成正比,比例系数为常数k.
(1)将全程燃料费用y(元)表示为静水中速度v(km/h)的函数;
(2)若s=100,p=10,q=110,k=2,为了使全程的燃料费用最少,轮船的实际行驶速度应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次函数f(x)=x2+(2t-1)x+1-2t.
(1)求证:对于任意t∈R,方程f(x)=1必有实数根;
(2)若
 <t<
<t< ,求证:方程f(x)=0在区间(-1,0)及
,求证:方程f(x)=0在区间(-1,0)及 内各有一个实数根.
内各有一个实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】某DVD光盘销售部每天的房租、人员工资等固定成本为300元,每张DVD光盘的进价是6元,销售单价与日均销售量的关系如表所示:
销售单价(元)
7
8
9
10
11
12
13
日均销售量(张)
480
440
400
360
320
280
240
(1)请根据以上数据作出分析,写出日均销售量P(x)(张)关于销售单价x(元)的函数关系式,并写出其定义域;
(2)问这个销售部销售的DVD光盘销售单价定为多少时才能使日均销售利润最大?最大销售利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A是同时符合以下性质的函数f(x)组成的集合:
①x∈[0,+∞),都有f(x)∈(1,4];②f(x)在[0,+∞)上是减函数.
(1)判断函数f1(x)=2-
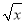 和f2(x)=1+3·
和f2(x)=1+3·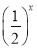 (x≥0)是否属于集合A,并简要说明理由;
(x≥0)是否属于集合A,并简要说明理由;(2)把(1)中你认为是集合A中的一个函数记为g(x),若不等式g(x)+g(x+2)≤k对任意的x≥0总成立,求实数k的取值范围.
相关试题

