【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求这20名工人年龄的众数与平均数;
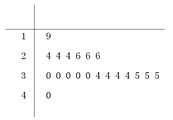
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
参考答案:
【答案】(1)30;(2)详见解析;(3)![]() .
.
【解析】试题分析:(1)利用车间![]() 名工人年龄数据表能求出这
名工人年龄数据表能求出这![]() 名工人年龄的众数和平均数.
名工人年龄的众数和平均数.
(2)利用车间![]() 名工人年龄数据表能作出茎叶图.
名工人年龄数据表能作出茎叶图.
(3) 记年龄为![]() 岁的三个人为
岁的三个人为![]() ;年龄为
;年龄为![]() 岁的三个人为
岁的三个人为![]() ,利用列举法能求出这
,利用列举法能求出这![]() 人均是
人均是![]() 岁的概率.
岁的概率.
试题解析:(1)由题意可知,这![]() 名工人年龄的众数是
名工人年龄的众数是![]() ,
,
这![]() 名工人年龄的平均数为:
名工人年龄的平均数为:
![]() .
.
(2)这![]() 名工人年龄的茎叶图如图所示:
名工人年龄的茎叶图如图所示:
(3)记年龄为![]() 岁的三个人为
岁的三个人为![]() ;年龄为
;年龄为![]() 岁的三个人为
岁的三个人为![]() ,则从这
,则从这![]() 人中随机抽取
人中随机抽取![]() 人的所有可能为:
人的所有可能为:
![]() ,
,
![]() ,
,
![]() 共
共![]() 种.
种.
满足题意的有![]() 种,
种,
故所求的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱锥P—ABC中,PC
 底面ABC,AB=BC,D、F分别为AC、PC的中点,DE
底面ABC,AB=BC,D、F分别为AC、PC的中点,DE AP于E。(1)求证:AP
AP于E。(1)求证:AP 平面BDE;(2)求证:平面BDE
平面BDE;(2)求证:平面BDE 平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。
平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
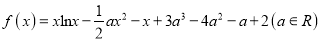 存在两个极值点.
存在两个极值点.(Ⅰ)求实数a的取值范围;
(Ⅱ)设
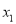 和
和 分别是
分别是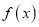 的两个极值点且
的两个极值点且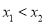 ,证明:
,证明: 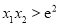 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log2(1-x),g(x)=log2(x+1),设F(x)=f(x)-g(x).
(1)判断函数F(x)的奇偶性;
(2)证明函数F(x)是减函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知斜三棱柱
 的底面是直角三角形,
的底面是直角三角形, ,侧棱与底面所成角为
,侧棱与底面所成角为 ,点
,点 在底面上身影
在底面上身影 落在
落在 上.
上.
(1)求证:
 平面
平面 ;
;(2)若点
 恰为
恰为 中点,且
中点,且 ,求
,求 的大小;
的大小;(3)若
 ,且当
,且当 时,求二面角
时,求二面角 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于命题
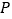 :存在一个常数
:存在一个常数 ,使得不等式
,使得不等式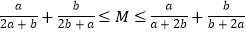 对任意正数
对任意正数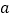 ,
, 恒成立.
恒成立.(1)试给出这个常数
 的值;
的值;(2)在(1)所得结论的条件下证明命题
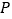 ;
; (3)对于上述命题,某同学正确地猜想了命题
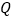 :“存在一个常数
:“存在一个常数 ,使得不等式
,使得不等式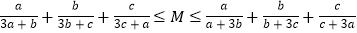 对任意正数
对任意正数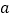 ,
, ,
,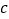 恒成立.”观察命题
恒成立.”观察命题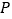 与命题
与命题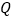 的规律,请猜想与正数
的规律,请猜想与正数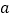 ,
, ,
,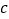 ,
,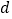 相关的命题.
相关的命题. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
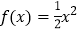 ,
,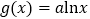 .
.(1)若曲线
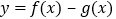 在
在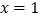 处的切线的方程为
处的切线的方程为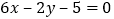 ,求实数
,求实数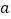 的值;
的值;(2)设
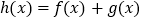 ,若对任意两个不等的正数
,若对任意两个不等的正数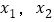 ,都有
,都有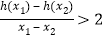 恒成立,求实数
恒成立,求实数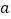 的取值范围;
的取值范围;(3)若在
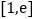 上存在一点
上存在一点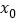 ,使得
,使得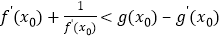 成立,求实数
成立,求实数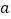 的取值范围.
的取值范围.
相关试题

