【题目】如图,在底面为矩形的四棱锥![]() 中,
中, ![]() .
.
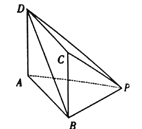
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
, ![]() ,
, ![]() ,求二面角
,求二面角![]() 的大小.
的大小.
参考答案:
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:
(1)由题意结合几何关系可证得![]() 平面
平面![]() ,结合面面垂直的判断定理即可证得平面
,结合面面垂直的判断定理即可证得平面![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,结合半平面的法向量可得二面角![]() 的大小是
的大小是![]() .
.
试题解析:
(1)证明:由已知四边形![]() 为矩形,得
为矩形,得![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)解:以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() .
.
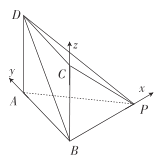
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,则
,则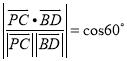 ,即
,即![]() ,
,
解得![]() (
(![]() 舍去).
舍去).
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则![]() ,即
,即![]() ,
,
可取![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则![]() 即
即![]() ,
,
可取![]() ,所以
,所以![]() ,
,
由图可知二面角![]() 为锐角,所以二面角
为锐角,所以二面角![]() 的大小为
的大小为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知无穷数列
 的首项
的首项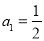 ,
, 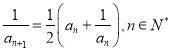 .
.(Ⅰ)证明:
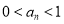 ;
;(Ⅱ) 记
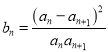 ,
, 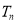 为数列
为数列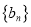 的前
的前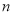 项和,证明:对任意正整数
项和,证明:对任意正整数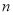 ,
, 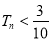 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 的焦点在抛物线
的焦点在抛物线 上,点
上,点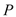 是抛物线
是抛物线 上的动点.
上的动点.(Ⅰ)求抛物线
 的方程及其准线方程;
的方程及其准线方程;(Ⅱ)过点
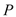 作抛物线
作抛物线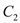 的两条切线,
的两条切线,  、
、 分别为两个切点,求
分别为两个切点,求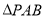 面积的最小值.
面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,  ,
,  ∥
∥ ,且
,且
 ,
,  ,
,  .
.
(Ⅰ)求证:平面
 ⊥平面
⊥平面 ;
;(Ⅱ)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
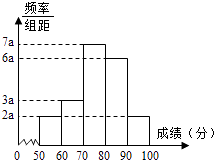
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列{an}中,a2+a7=﹣23,a3+a8=﹣29.
(1)求数列{an}的通项公式;
(2)设数列{an+bn}是首项为1,公比为c的等比数列,求{bn}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在D上的函数f(x)若同时满足:①存在M>0,使得对任意的x1 , x2∈D,都有|f(x1)﹣f(x2)|<M;②f(x)的图象存在对称中心.则称f(x)为“P﹣函数”.
已知函数f1(x)=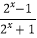 和f2(x)=lg(
和f2(x)=lg( 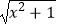 ﹣x),则以下结论一定正确的是( )
﹣x),则以下结论一定正确的是( )
A.f1(x)和 f2(x)都是P﹣函数
B.f1(x)是P﹣函数,f2(x)不是P﹣函数
C.f1(x)不是P﹣函数,f2(x)是P﹣函数
D.f1(x)和 f2(x)都不是P﹣函数
相关试题

