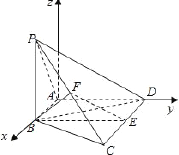
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() ∥
∥![]() ,且
,且![]()
![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
参考答案:
【答案】(I)证明见解析;(Ⅱ)![]() .
.
【解析】试题分析:(1)证明面面垂直,一般利用面面垂直判定定理,即从线面垂直进行论证,而线面垂直证明,往往需要多次利用线线垂直与线面垂直的转化,而线线垂直,有时可利用平几条件进行寻找与论证,如本题取![]() 中点E,利用平几知识得到四边形
中点E,利用平几知识得到四边形![]() 是矩形,从而得到
是矩形,从而得到![]() ,而易得
,而易得![]() ,因此
,因此![]() ,进而有平面
,进而有平面![]() 平面
平面![]() ;(2)利用空间向量求线面角,首先建立空间直角坐标系:以A 为原点,
;(2)利用空间向量求线面角,首先建立空间直角坐标系:以A 为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,建立空间直角坐标角系,设出各点坐标,利用方程组解出面的法向量,利用向量数量积求夹角,最后根据线面角与向量夹角互余得结论
轴,建立空间直角坐标角系,设出各点坐标,利用方程组解出面的法向量,利用向量数量积求夹角,最后根据线面角与向量夹角互余得结论
试题解析:解:证明:(1)![]() 为
为![]() 中点,
中点, ![]() ,
, ![]() ,且
,且![]() 四边形
四边形![]() 是矩形,
是矩形, ![]() ,又
,又![]() 平面
平面![]() ,且
,且![]() ,
,![]() 在平面
在平面![]() 中,
中, ![]() 平面
平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
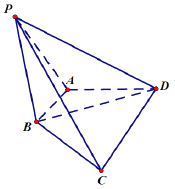
(2)以A 为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,建立空间直角坐标角系,
轴,建立空间直角坐标角系,
![]() ,
,
![]() 则
则![]()
![]()
设平面![]() 的法向量
的法向量![]() ,则
,则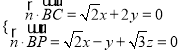 ,取
,取![]() ,得
,得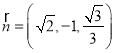 ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
, 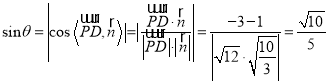 ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
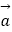 =(sin2x,2cos2x﹣1),
=(sin2x,2cos2x﹣1), 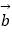 =(sinθ,cosθ)(0<θ<π),函数f(x)=
=(sinθ,cosθ)(0<θ<π),函数f(x)= 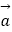
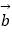 的图象经过点(
的图象经过点(  ,1).
,1).
(1)求θ及f(x)的最小正周期;
(2)当x∈ 时,求f(x)的最大值和最小值.
时,求f(x)的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知无穷数列
 的首项
的首项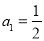 ,
, 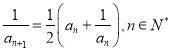 .
.(Ⅰ)证明:
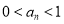 ;
;(Ⅱ) 记
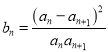 ,
, 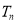 为数列
为数列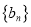 的前
的前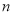 项和,证明:对任意正整数
项和,证明:对任意正整数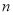 ,
, 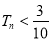 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 的焦点在抛物线
的焦点在抛物线 上,点
上,点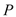 是抛物线
是抛物线 上的动点.
上的动点.(Ⅰ)求抛物线
 的方程及其准线方程;
的方程及其准线方程;(Ⅱ)过点
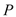 作抛物线
作抛物线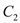 的两条切线,
的两条切线,  、
、 分别为两个切点,求
分别为两个切点,求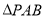 面积的最小值.
面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面为矩形的四棱锥
 中,
中,  .
.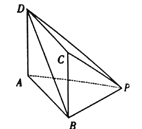
(1)证明:平面
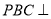 平面
平面 ;
;(2)若异面直线
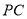 与
与 所成角为
所成角为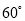 ,
,  ,
,  ,求二面角
,求二面角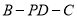 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
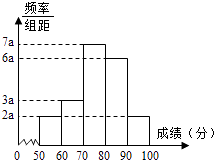
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列{an}中,a2+a7=﹣23,a3+a8=﹣29.
(1)求数列{an}的通项公式;
(2)设数列{an+bn}是首项为1,公比为c的等比数列,求{bn}的前n项和Sn .
相关试题

