【题目】已知无穷数列![]() 的首项
的首项![]() ,
, 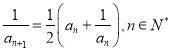 .
.
(Ⅰ)证明: ![]() ;
;
(Ⅱ) 记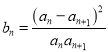 ,
, ![]() 为数列
为数列![]() 的前
的前![]() 项和,证明:对任意正整数
项和,证明:对任意正整数![]() ,
, ![]() .
.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析; (I)运用数学归纳法推理论证,
(Ⅱ)由已知![]() ,即
,即![]() ,可得数列
,可得数列![]() 为递增数列。
为递增数列。
又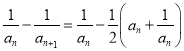
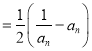 ,易知
,易知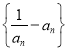 为递减数列,
为递减数列,
则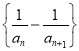 也为递减数列,故当
也为递减数列,故当![]() 时,
时, ![]()
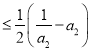
![]()
![]()
所以当![]() 时,
时, 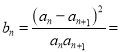
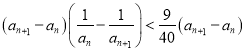
当![]() 时,
时, ![]() ,成立;
,成立;
当![]() 时,利用裂项求和法即可得证
时,利用裂项求和法即可得证
试题解析:(Ⅰ)证明:①当![]() 时显然成立;
时显然成立;
②假设当![]()
![]() 时不等式成立,即
时不等式成立,即![]() ,
,
那么当![]() 时,
时, 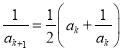
![]()
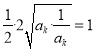 ,所以
,所以![]() ,
,
即![]() 时不等式也成立.
时不等式也成立.
综合①②可知, ![]() 对任意
对任意![]() 成立.
成立.
(Ⅱ)![]() ,即
,即![]() ,所以数列
,所以数列![]() 为递增数列。
为递增数列。
又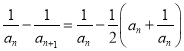
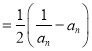 ,易知
,易知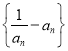 为递减数列,
为递减数列,
所以 也为递减数列,
也为递减数列,
所以当![]() 时,
时, ![]()
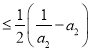
![]()
![]()
所以当![]() 时,
时, 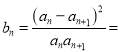
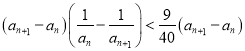
当![]() 时,
时, ![]() ,成立;
,成立;
当![]() 时,
时, ![]()
![]()
![]()
![]()
![]()
综上,对任意正整数![]() ,
, ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
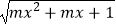 的定义域是一切实数,则m的取值范围是( )
的定义域是一切实数,则m的取值范围是( )
A.0<m≤4
B.0≤m≤1
C.m≥4
D.0≤m≤4 -
科目: 来源: 题型:
查看答案和解析>>【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
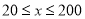 时,车流速度
时,车流速度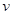 是车流密度
是车流密度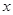 的一次函数.
的一次函数.(1)当
 时,求函数
时,求函数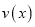 的表达式;
的表达式;(2)当车流密度
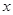 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)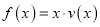 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
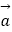 =(sin2x,2cos2x﹣1),
=(sin2x,2cos2x﹣1), 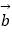 =(sinθ,cosθ)(0<θ<π),函数f(x)=
=(sinθ,cosθ)(0<θ<π),函数f(x)= 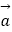
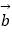 的图象经过点(
的图象经过点(  ,1).
,1).
(1)求θ及f(x)的最小正周期;
(2)当x∈ 时,求f(x)的最大值和最小值.
时,求f(x)的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 的焦点在抛物线
的焦点在抛物线 上,点
上,点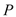 是抛物线
是抛物线 上的动点.
上的动点.(Ⅰ)求抛物线
 的方程及其准线方程;
的方程及其准线方程;(Ⅱ)过点
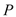 作抛物线
作抛物线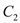 的两条切线,
的两条切线,  、
、 分别为两个切点,求
分别为两个切点,求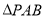 面积的最小值.
面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,  ,
,  ∥
∥ ,且
,且
 ,
,  ,
,  .
.
(Ⅰ)求证:平面
 ⊥平面
⊥平面 ;
;(Ⅱ)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
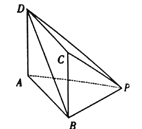
查看答案和解析>>【题目】如图,在底面为矩形的四棱锥
 中,
中,  .
.
(1)证明:平面
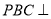 平面
平面 ;
;(2)若异面直线
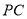 与
与 所成角为
所成角为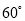 ,
,  ,
,  ,求二面角
,求二面角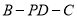 的大小.
的大小.
相关试题

