【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图: 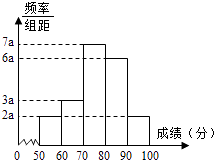
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率.
参考答案:
【答案】
(1)解:根据直方图知组距=10,由(2a+3a+6a+7a+2a)×10=1,解得a=0.005.
(2)解:成绩落在[50,60)中的学生人数为2×0.005×10×20=2,
成绩落在[60,70)中的学生人数为3×0.005×10×20=3.
(3)解:记成绩落在[50,60)中的2人为A,B,成绩落在[60,70)中的3人为C,D,E,则成绩在[50,70)的学生任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,
其中2人的成绩都在[60,70)中的基本事件有CD,CE,DE共3个,
故所求概率为P= ![]()
【解析】(1)根据频率分布直方图求出a的值;(2)由图可知,成绩在[50,60)和[60,70)的频率分别为0.1和0.15,用样本容量20乘以对应的频率,即得对应区间内的人数,从而求出所求.(3)分别列出满足[50,70)的基本事件,再找到在[60,70)的事件个数,根据古典概率公式计算即可.
【考点精析】根据题目的已知条件,利用频率分布直方图的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 的焦点在抛物线
的焦点在抛物线 上,点
上,点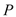 是抛物线
是抛物线 上的动点.
上的动点.(Ⅰ)求抛物线
 的方程及其准线方程;
的方程及其准线方程;(Ⅱ)过点
 作抛物线
作抛物线 的两条切线,
的两条切线,  、
、 分别为两个切点,求
分别为两个切点,求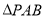 面积的最小值.
面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,  ,
,  ∥
∥ ,且
,且
 ,
,  ,
,  .
.
(Ⅰ)求证:平面
 ⊥平面
⊥平面 ;
;(Ⅱ)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面为矩形的四棱锥
 中,
中,  .
.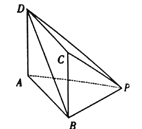
(1)证明:平面
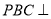 平面
平面 ;
;(2)若异面直线
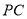 与
与 所成角为
所成角为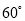 ,
,  ,
,  ,求二面角
,求二面角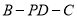 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列{an}中,a2+a7=﹣23,a3+a8=﹣29.
(1)求数列{an}的通项公式;
(2)设数列{an+bn}是首项为1,公比为c的等比数列,求{bn}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在D上的函数f(x)若同时满足:①存在M>0,使得对任意的x1 , x2∈D,都有|f(x1)﹣f(x2)|<M;②f(x)的图象存在对称中心.则称f(x)为“P﹣函数”.
已知函数f1(x)=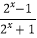 和f2(x)=lg(
和f2(x)=lg( 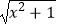 ﹣x),则以下结论一定正确的是( )
﹣x),则以下结论一定正确的是( )
A.f1(x)和 f2(x)都是P﹣函数
B.f1(x)是P﹣函数,f2(x)不是P﹣函数
C.f1(x)不是P﹣函数,f2(x)是P﹣函数
D.f1(x)和 f2(x)都不是P﹣函数 -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=|ax﹣1﹣1|在区间(a,3a﹣1)上单调递减,则实数a的取值范围是 .
相关试题

