【题目】如图,![]() 是平行四边形,
是平行四边形,![]() ,
,![]() 为
为![]() 的中点,且有
的中点,且有![]() ,现以
,现以![]() 为折痕,将
为折痕,将![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,且
的位置,且![]()
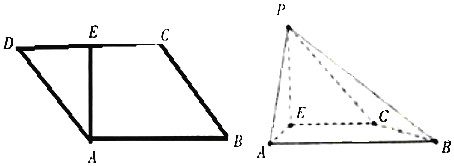
(1)证明:![]() 平面
平面![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的侧面积.
的侧面积.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先推导出![]() ,利用线面垂直的判定定理能证明
,利用线面垂直的判定定理能证明![]() 平面
平面![]() ;(2)由四棱锥
;(2)由四棱锥![]() 的体积为
的体积为![]() 求出
求出![]() ,由
,由![]() ,可得平
,可得平![]() 面
面![]() ,推导出
,推导出![]() ,分别求出4个侧面的面积即可求出四棱锥
,分别求出4个侧面的面积即可求出四棱锥![]() 的侧面积.
的侧面积.
(1)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴∠PEC=90°,即PE⊥EC,
又PE⊥AE,∴PE⊥面ABCE.
(2)由(1)得PE⊥面ABCE,
VP-ABCE=![]() ,
,
∴AE=1,∴PE⊥AB,又AB⊥AE,
∴AB⊥面PAE,∴AB⊥PA,∴PA=![]() ,
,
由题意得BC=PC=![]() ,PB=
,PB=![]() ,
,
△PBC中,由余弦定理得![]() ,
,
∴∠PCB=120°,
∴![]() ,
,
![]() ,
,![]() ,
,
∴四棱锥P-ABCE的侧面积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产某种产品的年固定成本为250万元,每生产
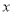 千件,需另投入成本
千件,需另投入成本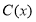 ,当年产量不足80千件时,
,当年产量不足80千件时,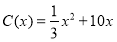 (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,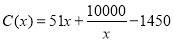 (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.(1)写出年利润
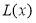 (万元)关于年产量
(万元)关于年产量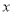 (千件)的函数解析式;
(千件)的函数解析式;(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0 , 且x0>0,则实数a的取值范围是( )
A.(1,+∞)
B.(2,+∞)
C.(﹣∞,﹣1)
D.(﹣∞,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
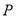 为抛物线
为抛物线 上一个动点,
上一个动点,  为圆
为圆 上一个动点,那么点
上一个动点,那么点 到点
到点 的距离与点
的距离与点 到抛物线的准线距离之和的最小值是( )
到抛物线的准线距离之和的最小值是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知标准方程下的椭圆
 的焦点在
的焦点在 轴上,且经过点
轴上,且经过点 ,它的一个焦点恰好与抛物线
,它的一个焦点恰好与抛物线 的焦点重合.椭圆
的焦点重合.椭圆 的上顶点为
的上顶点为 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 两点,连接
两点,连接 、
、 ,记直线
,记直线 的斜率分别为
的斜率分别为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , a1=1,an≠0,anan+1=λSn﹣1,其中λ为常数.
(1)证明:an+2﹣an=λ
(2)是否存在λ,使得{an}为等差数列?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
相关试题

