【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
参考答案:
【答案】D
【解析】
根据y与x的线性回归方程为 y=0.85x﹣85.71,则
![]() =0.85>0,y 与 x 具有正的线性相关关系,A正确;
=0.85>0,y 与 x 具有正的线性相关关系,A正确;
回归直线过样本点的中心(![]() ),B正确;
),B正确;
该大学某女生身高增加 1cm,预测其体重约增加 0.85kg,C正确;
该大学某女生身高为 170cm,预测其体重约为0.85×170﹣85.71=58.79kg,D错误.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
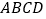 是平行四边形,
是平行四边形,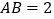 ,
,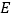 为
为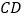 的中点,且有
的中点,且有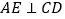 ,现以
,现以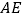 为折痕,将
为折痕,将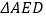 折起,使得点
折起,使得点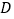 到达点
到达点 的位置,且
的位置,且
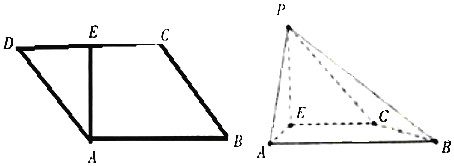
(1)证明:
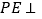 平面
平面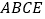 ;
;(2)若四棱锥
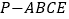 的体积为
的体积为 ,求四棱锥
,求四棱锥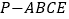 的侧面积.
的侧面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知标准方程下的椭圆
 的焦点在
的焦点在 轴上,且经过点
轴上,且经过点 ,它的一个焦点恰好与抛物线
,它的一个焦点恰好与抛物线 的焦点重合.椭圆
的焦点重合.椭圆 的上顶点为
的上顶点为 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 两点,连接
两点,连接 、
、 ,记直线
,记直线 的斜率分别为
的斜率分别为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , a1=1,an≠0,anan+1=λSn﹣1,其中λ为常数.
(1)证明:an+2﹣an=λ
(2)是否存在λ,使得{an}为等差数列?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率低于
 ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点p(1,m)在抛物线
 上,F为焦点,且
上,F为焦点,且 .
.(1)求抛物线C的方程;
(2)过点T(4,0)的直线
 交抛物线C于A,B两点,O为坐标原点,求
交抛物线C于A,B两点,O为坐标原点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
相关试题

