【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
参考答案:
【答案】(1)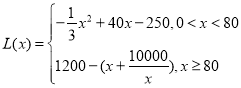 ;(2)100千件.
;(2)100千件.
【解析】
(1)分两种情况进行研究,当![]() 时,当
时,当![]() 时,分别根据年利润等于销售收入与成本的差,列出函数关系式,最后写成分段函数的形式,从而得到答案;(2)根据年利润的解析式,分段研究函数的最值,当
时,分别根据年利润等于销售收入与成本的差,列出函数关系式,最后写成分段函数的形式,从而得到答案;(2)根据年利润的解析式,分段研究函数的最值,当![]() 时,利用二次函数求最值,当
时,利用二次函数求最值,当![]() 时,利用基本不等式求最值,最后比较两个最值,即可得到答案.
时,利用基本不等式求最值,最后比较两个最值,即可得到答案.
(1)∵每件商品售价为0.05万元,
∴![]() 千件商品销售额为
千件商品销售额为![]() 万元,
万元,
①当![]() 时,根据年利润=销售收入-成本,
时,根据年利润=销售收入-成本,
∴![]() ;
;
②当![]() 时,根据年利润=销售收入-成本,
时,根据年利润=销售收入-成本,
∴![]()
综合①②可得,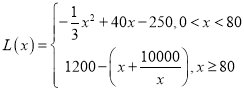 ;
;
(2)①当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() 取得最大值
取得最大值![]() 万元;
万元;
②当![]() 时,
时,![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() 万元.
万元.
综合①②,由于![]() ,
,
∴年产量为100千件时,该厂在这一商品的生产中所获利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】π为圆周率,e=2.71828…为自然对数的底数.
(1)求函数f(x)= 的单调区间;
的单调区间;
(2)求e3 , 3e , eπ , πe , 3π , π3这6个数中的最大数和最小数;
(3)将e3 , 3e , eπ , πe , 3π , π3这6个数按从小到大的顺序排列,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
 的解集记为D,有下列四个命题:
的解集记为D,有下列四个命题:
p1:(x,y)∈D,x+2y≥﹣2 p2:(x,y)∈D,x+2y≥2
p3:(x,y)∈D,x+2y≤3 p4:(x,y)∈D,x+2y≤﹣1
其中真命题是( )
A.p2 , p3
B.p1 , p4
C.p1 , p2
D.p1 , p3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
 中,
中, ,
, 为棱
为棱 的中点,
的中点, .
.
(1)证明:
 平面
平面 ;
;(2)设二面角
 的正切值为
的正切值为 ,
, ,
, ,求异面直线
,求异面直线 与
与 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0 , 且x0>0,则实数a的取值范围是( )
A.(1,+∞)
B.(2,+∞)
C.(﹣∞,﹣1)
D.(﹣∞,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
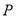 为抛物线
为抛物线 上一个动点,
上一个动点,  为圆
为圆 上一个动点,那么点
上一个动点,那么点 到点
到点 的距离与点
的距离与点 到抛物线的准线距离之和的最小值是( )
到抛物线的准线距离之和的最小值是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
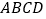 是平行四边形,
是平行四边形,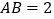 ,
, 为
为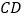 的中点,且有
的中点,且有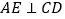 ,现以
,现以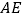 为折痕,将
为折痕,将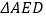 折起,使得点
折起,使得点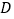 到达点
到达点 的位置,且
的位置,且
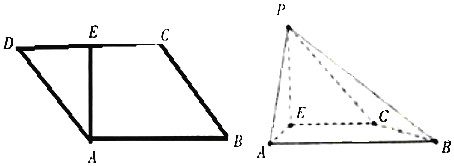
(1)证明:
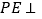 平面
平面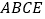 ;
;(2)若四棱锥
 的体积为
的体积为 ,求四棱锥
,求四棱锥 的侧面积.
的侧面积.
相关试题

