【题目】设函数![]()
(1)若![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,求
,求![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若![]() ,求证:在
,求证:在![]() 时,
时, ![]() .
.
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() .单调增区间为
.单调增区间为![]() ;
;
当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)先求出![]() ,通过
,通过![]() 在点
在点![]() 处的切线斜率,可得
处的切线斜率,可得![]() ,解得
,解得![]() ;(2)由(1)知:
;(2)由(1)知: ![]() ,结合导数分①
,结合导数分①![]() 、②
、②![]() 两种情况讨论分别令
两种情况讨论分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;;(3)通过变形,只需证明
的减区间;;(3)通过变形,只需证明![]() 即可,利用
即可,利用![]() ,根据指数函数及幂函数的性质、函数的单调性及零点判定定理即得到结论.
,根据指数函数及幂函数的性质、函数的单调性及零点判定定理即得到结论.
试题解析:(1)若![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
![]() ,
,
得![]() .
.
(2)由![]()
当![]() 时,令
时,令![]() 解得:
解得: ![]()
当![]() 变化时,
变化时, ![]() 随
随![]() 变化情况如表:
变化情况如表:
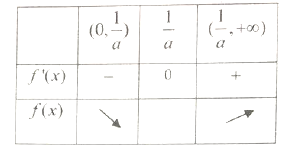
由表可知: ![]() 在
在![]() 上是单调减函数,在
上是单调减函数,在![]() 上是单调增函数
上是单调增函数
当![]() 时,
时, ![]() ,
, ![]() 的单调减区间为
的单调减区间为![]()
所以,当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() .单调增区间为
.单调增区间为![]()
当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]()
(3)当![]() 时,要证
时,要证![]() ,即证
,即证![]()
令![]() ,只需证
,只需证![]()
∵![]()
由指数函数及幕函数的性质知: ![]() 在
在![]() 上是增函数
上是增函数
∵![]() ,∴
,∴![]() 在
在![]() 内存在唯一的零点,
内存在唯一的零点,
也即![]() 在
在![]() 上有唯一零点
上有唯一零点
设![]() 的零点为
的零点为![]() ,则
,则![]() ,即
,即![]() ,
,
由![]() 的单调性知:
的单调性知:
当![]() 时,
时, ![]() ,
, ![]() 为减函数
为减函数
当![]() 时,
时, ![]() ,
, ![]() 为增函数,
为增函数,
所以当![]() 时.
时.
![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一张纸沿直线l对折一次后,点A(0,4)与点B(8,0)重叠,点C(6,8)与点D(m,n)重叠.
(1)求直线l的方程;
(2)求m+n的值;
(3)直线l上是否存在一点P,使得||PB|﹣|PC||存在最大值,如果存在,请求出最大值,以及此时点P的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱柱ABC﹣A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E、F分别在棱AA′,CC′上,且AE=C′F=2.
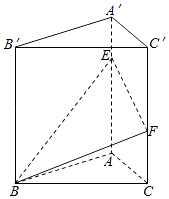
(1)求证:BB′⊥底面ABC;
(2)在棱A′B′上是否存在一点M,使得C′M∥平面BEF,若存在,求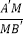 值,若不存在,说明理由;
值,若不存在,说明理由;
(3)求棱锥A′﹣BEF的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确命题的个数是( )
①若2b=a+c,则a,b,c成等差数列;
②“a,b,c成等比数列”的充要条件是“b2=ac”;
③若数列{an2}是等比数列,则数列{an}也是等比数列;
④若|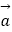 |=|
|=| 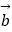 |,则
|,则 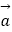 =
= 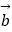 .
.
A.3
B.2
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系
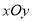 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为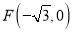 ,右顶点为
,右顶点为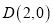 ,设点
,设点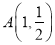 .
.(1)求该椭圆的标准方程;
(2)若
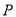 是椭圆上的动点,求线段
是椭圆上的动点,求线段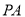 中点
中点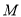 的轨迹方程;
的轨迹方程;(3)过原点
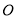 的直线交椭圆于点
的直线交椭圆于点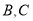 ,求
,求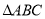 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 有三个不同的零点
有三个不同的零点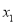 ,
, 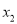 ,
, 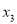 (其中
(其中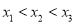 ),则
),则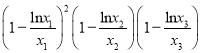 的值为( )
的值为( )A.
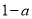 B.
B. 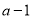 C.
C. 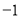 D.
D. 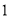
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆
 :
: 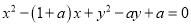 .
.(1)若圆
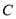 与
与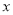 轴相切,求圆
轴相切,求圆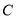 的方程;
的方程;(2)求圆心
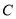 的轨迹方程;
的轨迹方程;(3)已知
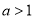 ,圆
,圆 与
与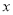 轴相交于两点
轴相交于两点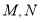 (点
(点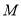 在点
在点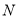 的左侧).过点
的左侧).过点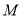 任作一条直线与圆
任作一条直线与圆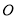 :
: 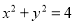 相交于两点
相交于两点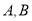 .问:是否存在实数
.问:是否存在实数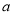 ,使得
,使得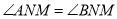 ?若存在,求出实数
?若存在,求出实数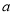 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
相关试题

