【题目】如图,圆![]() :
: ![]() .
.
(1)若圆![]() 与
与![]() 轴相切,求圆
轴相切,求圆![]() 的方程;
的方程;
(2)求圆心![]() 的轨迹方程;
的轨迹方程;
(3)已知![]() ,圆
,圆![]() 与
与![]() 轴相交于两点
轴相交于两点![]() (点
(点![]() 在点
在点![]() 的左侧).过点
的左侧).过点![]() 任作一条直线与圆
任作一条直线与圆![]() :
: ![]() 相交于两点
相交于两点![]() .问:是否存在实数
.问:是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() (3)存在
(3)存在![]() ,使得
,使得![]()
【解析】试题分析: ![]() 在圆的方程中,令
在圆的方程中,令![]() ,可得关于
,可得关于![]() 的一元二次方程的判别式等于零,由此求得
的一元二次方程的判别式等于零,由此求得![]() 的值,从而求得所求圆的方程。
的值,从而求得所求圆的方程。
(2)消去圆心坐标中的参数即可![]() 先求出
先求出![]() ,假设存在实数
,假设存在实数![]() ,当直线直线
,当直线直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,利用韦达定理,根据
,利用韦达定理,根据![]() 的斜率之和等于零求得
的斜率之和等于零求得![]() 的值,经过检验,当直线
的值,经过检验,当直线![]() 与
与![]() 轴垂直时,这个
轴垂直时,这个![]() 值仍然满足
值仍然满足![]() 从而得出结论
从而得出结论
解析:(1)由圆![]() 与
与![]() 轴相切,可知圆心的纵坐标的绝对值与半径相等.故先将圆
轴相切,可知圆心的纵坐标的绝对值与半径相等.故先将圆![]() 的方程化成标准方程为:
的方程化成标准方程为: ![]() ,由
,由![]() 求得
求得![]() .即可得到所求圆
.即可得到所求圆![]() 的方程为:
的方程为: ![]() ;
;
(2)求圆心![]() 点坐标为
点坐标为![]() ,则
,则![]()
![]() 圆心
圆心![]() 点的轨迹方程为
点的轨迹方程为![]()
(3)令![]() ,得
,得![]() ,即
,即![]() 所以
所以![]()
假设存在实数![]() ,当直线AB与
,当直线AB与![]() 轴不垂直时,设直线AB的方程为
轴不垂直时,设直线AB的方程为![]() ,
,
代入![]() 得,
得, ![]() ,设
,设![]() 从而
从而![]()
因为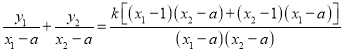
而![]()
![]()
![]()
因为![]() ,所以
,所以![]() ,即
,即![]() ,得
,得![]() .
.
当直线AB与![]() 轴垂直时,也成立.故存在
轴垂直时,也成立.故存在![]() ,使得
,使得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
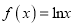 ,
, 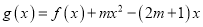 .
.(Ⅰ)当
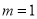 时,求曲线
时,求曲线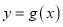 在
在 处的切线方程;
处的切线方程;(Ⅱ)当
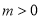 时,讨论函数
时,讨论函数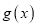 的单调性;
的单调性;(Ⅲ)设斜率为
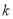 的直线与函数
的直线与函数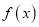 的图象交于
的图象交于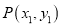 ,
, 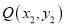 两点,其中
两点,其中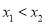 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂最近十年生产总量逐年上升,如表是部分统计数据:
年份
2008
2010
2012
2014
2016
生产总量(万吨)
(Ⅰ)利用所给数据求年生产总量与年份之间的回归直线方程
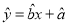 ;
;(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该厂2018年生产总量.
(回归直线的方程:
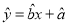 ,其中
,其中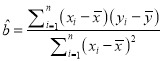 ,
, 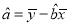 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
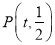 在椭圆
在椭圆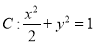 内,过
内,过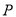 的直线
的直线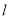 与椭圆
与椭圆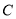 相交于A,B两点,且点
相交于A,B两点,且点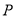 是线段AB的中点,O为坐标原点.
是线段AB的中点,O为坐标原点.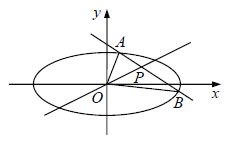
(Ⅰ)是否存在实数t,使直线
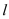 和直线OP的倾斜角互补?若存在,求出
和直线OP的倾斜角互补?若存在,求出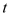 的值,若不存在,试说明理由;
的值,若不存在,试说明理由;(Ⅱ)求
 面积S的最大值.
面积S的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
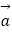 、
、 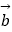 、
、 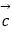 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 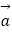 =(1,2)
=(1,2)
(1)若|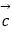 |=2
|=2 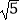 ,且
,且 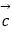 ∥
∥ 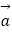 ,求
,求 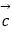 的坐标;
的坐标;
(2)若|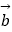 |=
|= 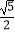 ,且
,且 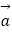 +2
+2 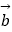 与2
与2 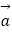 ﹣
﹣ 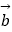 垂直,求v与
垂直,求v与 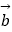 的夹角θ.
的夹角θ. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
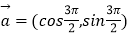 ,
, 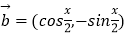 ,且
,且 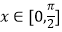 ,f(x)=
,f(x)= 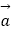
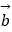 ﹣2λ|
﹣2λ| 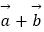 |(λ为常数),求:
|(λ为常数),求:
(1)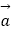
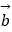 及|
及| 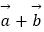 |;
|;
(2)若f(x)的最小值是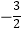 ,求实数λ的值.
,求实数λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱中
 ,点P,G分别是AD,EF的中点,已知
,点P,G分别是AD,EF的中点,已知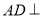 平面ABC,AD=EF=3,DE=DF=2.
平面ABC,AD=EF=3,DE=DF=2.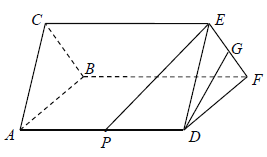
(Ⅰ)求证:DG⊥平面BCEF;
(Ⅱ)求PE与平面BCEF 所成角的正弦值.
相关试题

