【题目】已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为F(-![]() ,0),且过点D(2,0).
,0),且过点D(2,0).
(1)求该椭圆的标准方程;
(2)设点A(1,![]() ),若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
),若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
参考答案:
【答案】解:(1)由题意知椭圆的焦点在x轴上,设椭圆的标准方程是![]()
![]()
∵椭圆经过点D(2,0),左焦点为F(-![]() ,0),
,0),
∴a=2,c=![]() ,可得b=
,可得b=![]() =1
=1
因此,椭圆的标准方程为![]() .
.
(2)设点P的坐标是(x0 , y0),线段PA的中点为M(x,y),
由根据中点坐标公式,可得 ,整理得
,整理得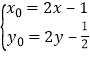 ,
,
∵点P(x0 , y0)在椭圆上,
∴可得![]() ,化简整理得
,化简整理得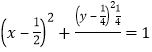 ,
,
由此可得线段PA中点M的轨迹方程是![]() .
.
【解析】(1)设椭圆方程为![]()
![]() , 根据题意可得a=2且c=
, 根据题意可得a=2且c=![]() , 从而b=
, 从而b=![]() =1,得到椭圆的标准方程;
=1,得到椭圆的标准方程;
(2)设点P(x0 , y0),线段PA的中点为M(x,y),根据中点坐标公式将x0、y0表示成关于x、y的式子,将P(x0 , y0)关于x、y的坐标形式代入已知椭圆的方程,化简整理即可得到线段PA的中点M的轨迹方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a为实数,p:点M(1,1)在圆(x+a)2+(y﹣a)2=4的内部; q:x∈R,都有x2+ax+1≥0.
(1)若p为真命题,求a的取值范围;
(2)若q为假命题,求a的取值范围;
(3)若“p且q”为假命题,且“p或q”为真命题,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组中的两个函数是同一函数的为( )
·(1)y=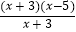 ,y=x﹣5;
,y=x﹣5;
·(2)y=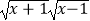 ,y=
,y= 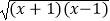 ;
;
·(3)y=|x|,y=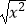 ;
;
·(4)y=x,y=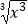 ;
;
·(5)y=(2x﹣5)2 , y=|2x﹣5|.
A.(1),(2)
B.(2),(3)
C.(3),(5)
D.(3),(4) -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆的中心在原点,对称轴为坐标轴,且长轴长是短轴长的2倍.又点P(4,1)在椭圆上,求该椭圆的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知指数函数y=ax在[0,1]上的最大值与最小值的差为
 ,则实数a的值为( )
,则实数a的值为( )
A.
B.
C.
或
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
①函数y=|x|与函数y=(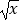 )2表示同一个函数;
)2表示同一个函数;
②奇函数的图象一定通过直角坐标系的原点;
③若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];
④设函数f(x)是在区间[a,b]上图象连续的函数,且f(a)f(b)<0,则方程f(x)=0在区间[a,b]上至少有一实根;
其中正确命题的序号是(填上所有正确命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知M={(x,y)|
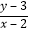 =3},N={(x,y)|ax+2y+a=0}且M∩N=,则a=( )
=3},N={(x,y)|ax+2y+a=0}且M∩N=,则a=( )
A.﹣6或﹣2
B.﹣6
C.2或﹣6
D.﹣2
相关试题

