【题目】给出下列四个命题:
①函数y=|x|与函数y=( ![]() )2表示同一个函数;
)2表示同一个函数;
②奇函数的图象一定通过直角坐标系的原点;
③若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];
④设函数f(x)是在区间[a,b]上图象连续的函数,且f(a)f(b)<0,则方程f(x)=0在区间[a,b]上至少有一实根;
其中正确命题的序号是(填上所有正确命题的序号)
参考答案:
【答案】④
【解析】解:①函数y=|x|的定义域为R,函数y=( ![]() )2定义域为[0,+∞),两函数的定义域不同,不是同一函数,①错误
)2定义域为[0,+∞),两函数的定义域不同,不是同一函数,①错误
②函数y= ![]() 为奇函数,但其图象不过坐标原点,②错误
为奇函数,但其图象不过坐标原点,②错误
③∵函数f(x)的定义域为[0,2],要使函数f(2x)有意义,需0≤2x≤2,即x∈[0,1],故函数f(2x)的定义域为[0,1],错误;
④函数f(x)是在区间[a.b]上图象连续的函数,f(a)f(b)<0,则方程f(x)=0在区间[a,b]上至少有一实根,④正确.
所以答案是④.
【考点精析】根据题目的已知条件,利用函数的概念及其构成要素的相关知识可以得到问题的答案,需要掌握函数三要素是定义域,对应法则和值域,而定义域和对应法则是起决定作用的要素,因为这二者确定后,值域也就相应得到确定,因此只有定义域和对应法则二者完全相同的函数才是同一函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆的中心在原点,对称轴为坐标轴,且长轴长是短轴长的2倍.又点P(4,1)在椭圆上,求该椭圆的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为F(-
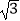 ,0),且过点D(2,0).
,0),且过点D(2,0).
(1)求该椭圆的标准方程;
(2)设点A(1, ),若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
),若P是椭圆上的动点,求线段PA的中点M的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知指数函数y=ax在[0,1]上的最大值与最小值的差为
 ,则实数a的值为( )
,则实数a的值为( )
A.
B.
C.
或
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知M={(x,y)|
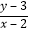 =3},N={(x,y)|ax+2y+a=0}且M∩N=,则a=( )
=3},N={(x,y)|ax+2y+a=0}且M∩N=,则a=( )
A.﹣6或﹣2
B.﹣6
C.2或﹣6
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:x∈(﹣∞,0),2x<3x;命题q:x∈(0,
 ),tanx>sinx,则下列命题为真命题的是( )
),tanx>sinx,则下列命题为真命题的是( )
A.p∧q
B.p∨(﹁q)
C.(﹁p)∧q
D.p∧(﹁q) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集U=R,集合A={x|x<﹣4,或x>2},B={x|﹣1≤2x﹣1﹣2≤6}.
(1)求A∩B、(UA)∪(UB);
(2)若集合M={x|2k﹣1≤x≤2k+1}是集合A的子集,求实数k的取值范围.
相关试题

