【题目】已知a为实数,p:点M(1,1)在圆(x+a)2+(y﹣a)2=4的内部; q:x∈R,都有x2+ax+1≥0.
(1)若p为真命题,求a的取值范围;
(2)若q为假命题,求a的取值范围;
(3)若“p且q”为假命题,且“p或q”为真命题,求a的取值范围.
参考答案:
【答案】解:(1)∵p:点M(1,1)在圆(x+a)2+(y﹣a)2=4的内部
∴(1+a)2+(1﹣a)2<4,解得﹣1<a<1,
故p为真命题时a的取值范围为(﹣1,1).
(2)∵q:x∈R,都有x2+ax+1≥0
∴若q为真命题,则△=a2﹣4≤0,解得﹣2≤a≤2,
故q为假命题时a的取值范围(﹣∞,﹣2)∪(2,+∞).
(3)∵“p且q”为假命题,且“p或q”为真命题
∴p与q一真一假,从而
①当p真q假时有![]() ,无解;
,无解;
②当p假q真时有![]() ,解得﹣2≤a≤﹣1或1≤a≤2.
,解得﹣2≤a≤﹣1或1≤a≤2.
∴实数a的取值范围是[﹣2,﹣1]∪[1,2].
【解析】对于命题p为真,要利用点与圆的位置关系;对于命题q为真,要利用一元二次函数图象的特点,最后利用复合命题真假解决.
【考点精析】利用复合命题和复合命题的真假对题目进行判断即可得到答案,需要熟知由简单命题和逻辑联结词“或”、“且”、“非”构成的命题是复合命题;构成复合命题的形式:p或q(记作“p∨q” );p且q(记作“p∧q” );非p(记作“┑q” );“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的各项均为正数,且Sn=
 +
+  +…+
+…+  ,S2=
,S2=  ,S3=
,S3=  .设[x]表示不大于x的最大整数(如[2.10]=2,[0.9]=0).
.设[x]表示不大于x的最大整数(如[2.10]=2,[0.9]=0).
(1)试求数列{an}的通项;
(2)求T=[log21]+[log22]+[log23]+…+[log2( ﹣1)]+[log2(
﹣1)]+[log2(  )]关于n的表达式.
)]关于n的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】设复数z=a+i(i是虚数单位,a∈R,a>0),且|z|=
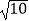 .
.
(Ⅰ)求复数z;
(Ⅱ)在复平面内,若复数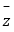 +
+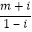 (m∈R)对应的点在第四象限,求实数m取值范围.
(m∈R)对应的点在第四象限,求实数m取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】命题p:函数y=log2(x2﹣2x)的单调增区间是[1,+∞),命题q:函数y=
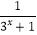 的值域为(0,1),下列命题是真命题的为( )
的值域为(0,1),下列命题是真命题的为( )
A.p∧q
B.p∨q
C.p∧(¬q)
D.¬q -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组中的两个函数是同一函数的为( )
·(1)y=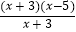 ,y=x﹣5;
,y=x﹣5;
·(2)y=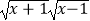 ,y=
,y= 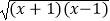 ;
;
·(3)y=|x|,y=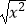 ;
;
·(4)y=x,y=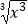 ;
;
·(5)y=(2x﹣5)2 , y=|2x﹣5|.
A.(1),(2)
B.(2),(3)
C.(3),(5)
D.(3),(4) -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆的中心在原点,对称轴为坐标轴,且长轴长是短轴长的2倍.又点P(4,1)在椭圆上,求该椭圆的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为F(-
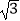 ,0),且过点D(2,0).
,0),且过点D(2,0).
(1)求该椭圆的标准方程;
(2)设点A(1, ),若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
),若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
相关试题

