【题目】一个抛物线型的拱桥,当水面离拱顶2 m时,水宽4 m,若水面下降1 m,求水的宽度.
参考答案:
【答案】![]()
【解析】试题分析:先根据抛物线顶点为坐标原点建立直角坐标系,根据条件得抛物线上一点坐标代入可得抛物线方程,再令对应y值可得横坐标,根据水的宽度与横坐标关系可得结果.
试题解析:解:如图建立直角坐标系.
 设抛物线的方程为x2=-2py,
设抛物线的方程为x2=-2py,
∵水面离拱顶2 m时,
水面宽4 m,
∴点(2,-2)在抛物线上,
∴4=4p,∴p=1.∴x2=-2y,
∵水面下降1 m,即y=-3,而y=-3时,x=±![]() ,
,
∴水面宽为2![]() m.
m.
即若水面下降1 m,水面的宽度为2![]() m.
m.
点睛;抛物线的几何特性在实际中应用广泛,解决此类问题的关键是根据题意(一般是根据题中所给图形)建立适当的直角坐标系,设出抛物线的标准方程,依据题意得到抛物线上一点的坐标,从而求出抛物线方程,进而解决实际问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD,

(Ⅰ)求证:平面PED⊥平面PAC;
(Ⅱ)若直线PE与平面PAC所成的角的正弦值为 ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
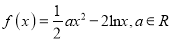 .
.(1)求函数
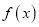 的单调区间;
的单调区间;(2)已知点
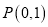 和函数
和函数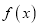 图像上动点
图像上动点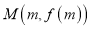 ,对任意
,对任意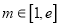 ,直线
,直线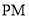 倾斜角都是钝角,求
倾斜角都是钝角,求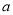 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某房地产开发公司计划在一楼区内建造一个长方形公园
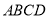 ,公园由长方形的休闲区
,公园由长方形的休闲区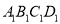 (阴影部分)和环公园人行道组成.已知休闲区
(阴影部分)和环公园人行道组成.已知休闲区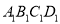 的面积为4000平方米,人行道的宽分别为4米和10米.
的面积为4000平方米,人行道的宽分别为4米和10米.(1)若设休闲区的长
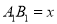 米,求公园
米,求公园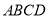 所占面积
所占面积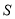 关于
关于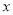 的函数
的函数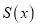 的解析式;
的解析式;(2)要使公园所占面积最小,休闲区
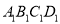 的长和宽该如何设计?
的长和宽该如何设计?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列条件,分别求抛物线的标准方程:
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,AF=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知椭圆C:
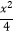 +y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N.
+y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N. 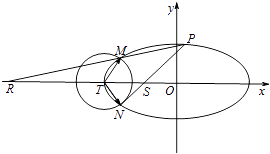
(1)求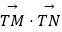 的最小值;
的最小值;
(2)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:丨OR丨丨OS丨为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
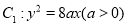 ,直线
,直线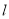 倾斜角是
倾斜角是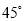 且过抛物线
且过抛物线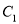 的焦点,直线
的焦点,直线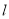 被抛物线
被抛物线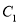 截得的线段长是16,双曲线
截得的线段长是16,双曲线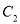 :
: 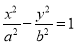 的一个焦点在抛物线
的一个焦点在抛物线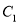 的准线上,则直线
的准线上,则直线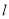 与
与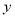 轴的交点
轴的交点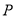 到双曲线
到双曲线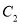 的一条渐近线的距离是( )
的一条渐近线的距离是( )A. 2 B.
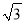 C.
C. 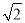 D. 1
D. 1
相关试题

