【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)已知点![]() 和函数
和函数![]() 图像上动点
图像上动点![]() ,对任意
,对任意![]() ,直线
,直线![]() 倾斜角都是钝角,求
倾斜角都是钝角,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)先求函数的定义域,然后求导,利用导数大于0或导数小于0,得到关于x的不等式,解之即可;注意解不等式时要结合对应的函数图象来解;
(2)因为对任意m∈[1,e],直线PM倾斜角都是钝角,所以问题转化为导数值小于0恒成立的问题,对于导函数小于0在区间[1,e]上恒成立,则问题转化为函数的最值问题,即函数f′(x)<0恒成立,通过化简最终转化为f(m)<1在区间[1,e]上恒成立,再通过研究f(x)在[1,e]上的单调性求最值,结合(Ⅰ)的结果即可解决问题.注意分类讨论的标准的确定.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,解得
,解得![]() 故
故![]() 在
在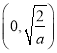 上单调递减,在
上单调递减,在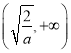 上单调递增.
上单调递增.
(2)因为对任意的![]() ,直线
,直线![]() 倾斜角都是钝角,即对任意的
倾斜角都是钝角,即对任意的![]() ,
, ![]() ,即
,即![]() ,即
,即![]() .
.
因为![]() ,令
,令![]() ,
,
(i)当![]() 时,由(1)知,
时,由(1)知, ![]() 在
在![]() 上单调递减
上单调递减![]() ,则由
,则由![]() ,故
,故![]() ,此时
,此时![]() 满足.
满足.
(ii)当![]() 时,令
时,令![]() ,得
,得![]() ,当
,当![]() 时,即
时,即![]() ,函数
,函数![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 的最大值为
的最大值为![]() ,解得
,解得![]() 与
与![]() 矛盾.
矛盾.
当![]() 时,即
时,即![]() ,函数
,函数![]() 在
在![]() 上单调递减,故
上单调递减,故![]() 的最大值为
的最大值为![]() ,得
,得![]() ,此时
,此时![]() .
.
当![]() 时,即
时,即![]() ,函数
,函数![]() 在
在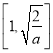 上单调递减,在
上单调递减,在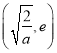 上单调递增,故
上单调递增,故![]() 在
在![]() 的最大值为
的最大值为![]() 或
或![]() ,
,
所以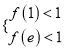 ,即
,即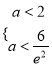 ,故
,故![]() ,综上,
,综上, ![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
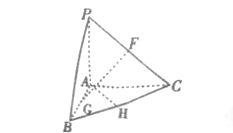
查看答案和解析>>【题目】如图,在三棱锥
 中,
中, 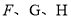 分别是
分别是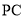 、
、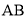 、
、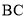 的中点,
的中点, 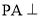 平面
平面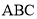 ,
, 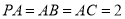 ,二面角
,二面角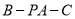 为
为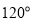 .
.
(1)证明:
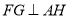 ;
;(2)求二面角
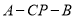 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
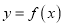 在实数集
在实数集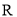 上的图象是连续不断的,且对任意实数
上的图象是连续不断的,且对任意实数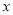 存在常数
存在常数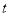 使得
使得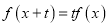 恒成立,则称
恒成立,则称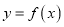 是一个“关于
是一个“关于 函数”.现有下列“关于
函数”.现有下列“关于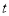 函数”的结论:
函数”的结论:①常数函数是“关于
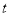 函数”;
函数”;②正比例函数必是一个“关于
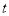 函数”;
函数”;③“关于
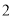 函数”至少有一个零点;
函数”至少有一个零点;④
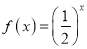 是一个“关于
是一个“关于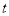 函数”.
函数”.其中正确结论的序号是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD,

(Ⅰ)求证:平面PED⊥平面PAC;
(Ⅱ)若直线PE与平面PAC所成的角的正弦值为 ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某房地产开发公司计划在一楼区内建造一个长方形公园
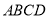 ,公园由长方形的休闲区
,公园由长方形的休闲区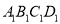 (阴影部分)和环公园人行道组成.已知休闲区
(阴影部分)和环公园人行道组成.已知休闲区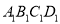 的面积为4000平方米,人行道的宽分别为4米和10米.
的面积为4000平方米,人行道的宽分别为4米和10米.(1)若设休闲区的长
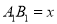 米,求公园
米,求公园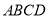 所占面积
所占面积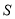 关于
关于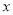 的函数
的函数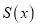 的解析式;
的解析式;(2)要使公园所占面积最小,休闲区
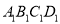 的长和宽该如何设计?
的长和宽该如何设计?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个抛物线型的拱桥,当水面离拱顶2 m时,水宽4 m,若水面下降1 m,求水的宽度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列条件,分别求抛物线的标准方程:
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,AF=5.
相关试题

