【题目】已知抛物线![]() ,直线
,直线![]() 倾斜角是
倾斜角是![]() 且过抛物线
且过抛物线![]() 的焦点,直线
的焦点,直线![]() 被抛物线
被抛物线![]() 截得的线段长是16,双曲线
截得的线段长是16,双曲线![]() :
: ![]() 的一个焦点在抛物线
的一个焦点在抛物线![]() 的准线上,则直线
的准线上,则直线![]() 与
与![]() 轴的交点
轴的交点![]() 到双曲线
到双曲线![]() 的一条渐近线的距离是( )
的一条渐近线的距离是( )
A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
参考答案:
【答案】D
【解析】抛物线的焦点为![]() ,由弦长计算公式有
,由弦长计算公式有![]() ,所以抛物线的标线方程为
,所以抛物线的标线方程为![]() ,准线方程为
,准线方程为![]() ,故双曲线的一个焦点坐标为
,故双曲线的一个焦点坐标为![]() ,即
,即![]() ,所以
,所以![]() ,渐近线方程为
,渐近线方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,所以点
,所以点![]() ,点P到双曲线的一条渐近线的距离为
,点P到双曲线的一条渐近线的距离为![]() ,选D.
,选D.
点睛: 本题主要考查了抛物线与双曲线的简单几何性质, 属于中档题. 先由直线过抛物线的焦点,求出弦长,由弦长求出![]() 的值,根据双曲线中
的值,根据双曲线中![]() 的关系求出
的关系求出![]() ,渐近线方程等,由点到直线距离公式求出点P到双曲线的一条渐近线的距离.
,渐近线方程等,由点到直线距离公式求出点P到双曲线的一条渐近线的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个抛物线型的拱桥,当水面离拱顶2 m时,水宽4 m,若水面下降1 m,求水的宽度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列条件,分别求抛物线的标准方程:
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,AF=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知椭圆C:
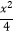 +y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N.
+y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N. 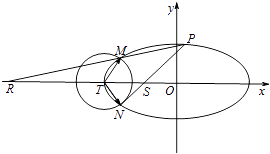
(1)求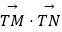 的最小值;
的最小值;
(2)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:丨OR丨丨OS丨为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x(lnx﹣ax).
(1)a= 时,求f(x)在点(1,f(1))处的切线方程;
时,求f(x)在点(1,f(1))处的切线方程;
(2)若f(x)存在两个不同的极值x1 , x2 , 求a的取值范围;
(3)在(2)的条件下,求f(x)在(0,a]上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)证明:函数
 在区间
在区间 上是减函数;
上是减函数;(2)当
 时,证明:函数
时,证明:函数 只有一个零点.
只有一个零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
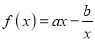 ,曲线
,曲线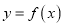 在点
在点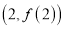 处的切线方程为
处的切线方程为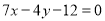 .
.(1)求
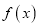 的解析式;
的解析式;(2)设
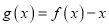 ,证明:函数
,证明:函数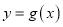 图象上任一点处的切线与两坐标轴所围成的三角形面积为定值,并求此定值.
图象上任一点处的切线与两坐标轴所围成的三角形面积为定值,并求此定值.
相关试题

