【题目】根据下列条件,分别求抛物线的标准方程:
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,AF=5.
参考答案:
【答案】(1)y2=-12x.(2)y2=±2x或y2=±18x.
【解析】试题分析:(1)先将双曲线方程化为标准方程,根据方程可得左顶点,即得抛物线焦点,根据焦点坐标直接写出抛物线标准方程(2)根据焦点位置可设抛物线标准方程形式,设A点坐标,根据抛物线定义以及点在抛物线上列方程组解得p,即得抛物线方程
试题解析:解:(1)双曲线方程化为![]() -
-![]() =1,左顶点为(-3,0),由题意设抛物线方程为y2=-2px(p>0),且
=1,左顶点为(-3,0),由题意设抛物线方程为y2=-2px(p>0),且![]() =-3,∴p=6,∴方程为y2=-12x.
=-3,∴p=6,∴方程为y2=-12x.
(2)设所求焦点在x轴上的抛物线的方程为
y2=2px(p≠0),A(m,-3),
由抛物线定义,得5=AF=![]() .
.
又(-3)2=2pm,∴p=±1或p=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
点睛; 待定系数法求抛物线的标准方程
(1)根据抛物线焦点是在x轴上还是在y轴上,设出相应形式的标准方程,然后根据条件确定关于p的方程,解出p,从而写出抛物线的标准方程.
(2)当焦点位置不确定时,有两种方法解决.一种是分情况讨论,注意要对四种形式的标准方程进行讨论,对于焦点在x轴上的抛物线,为避免开口方向不确定可分为y2=2px(p>0)和y2=-2px(p>0)两种情况求解.另一种是设成y2=mx(m≠0),若m>0,开口向右;若m<0,开口向左;若m有两个解,则抛物线的标准方程有两个.同理,焦点在y轴上的抛物线可以设成x2=my(m≠0).如果不确定焦点所在的坐标轴,应考虑上述两种情况设方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
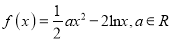 .
.(1)求函数
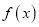 的单调区间;
的单调区间;(2)已知点
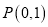 和函数
和函数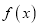 图像上动点
图像上动点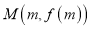 ,对任意
,对任意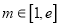 ,直线
,直线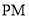 倾斜角都是钝角,求
倾斜角都是钝角,求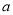 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某房地产开发公司计划在一楼区内建造一个长方形公园
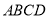 ,公园由长方形的休闲区
,公园由长方形的休闲区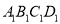 (阴影部分)和环公园人行道组成.已知休闲区
(阴影部分)和环公园人行道组成.已知休闲区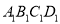 的面积为4000平方米,人行道的宽分别为4米和10米.
的面积为4000平方米,人行道的宽分别为4米和10米.(1)若设休闲区的长
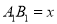 米,求公园
米,求公园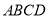 所占面积
所占面积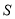 关于
关于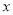 的函数
的函数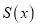 的解析式;
的解析式;(2)要使公园所占面积最小,休闲区
 的长和宽该如何设计?
的长和宽该如何设计?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个抛物线型的拱桥,当水面离拱顶2 m时,水宽4 m,若水面下降1 m,求水的宽度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知椭圆C:
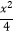 +y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N.
+y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N. 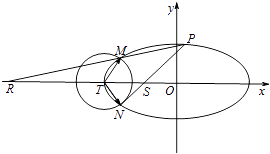
(1)求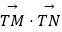 的最小值;
的最小值;
(2)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:丨OR丨丨OS丨为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
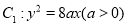 ,直线
,直线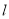 倾斜角是
倾斜角是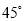 且过抛物线
且过抛物线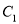 的焦点,直线
的焦点,直线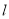 被抛物线
被抛物线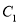 截得的线段长是16,双曲线
截得的线段长是16,双曲线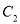 :
: 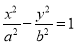 的一个焦点在抛物线
的一个焦点在抛物线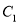 的准线上,则直线
的准线上,则直线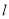 与
与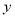 轴的交点
轴的交点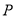 到双曲线
到双曲线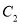 的一条渐近线的距离是( )
的一条渐近线的距离是( )A. 2 B.
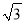 C.
C. 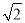 D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x(lnx﹣ax).
(1)a= 时,求f(x)在点(1,f(1))处的切线方程;
时,求f(x)在点(1,f(1))处的切线方程;
(2)若f(x)存在两个不同的极值x1 , x2 , 求a的取值范围;
(3)在(2)的条件下,求f(x)在(0,a]上的最小值.
相关试题

