【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD, 
(Ⅰ)求证:平面PED⊥平面PAC;
(Ⅱ)若直线PE与平面PAC所成的角的正弦值为 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.
参考答案:
【答案】解:(Ⅰ)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,AB⊥PA ∴PA⊥平面ABCD
结合AB⊥AD,可得
分别以AB、AD、AP为x轴、y轴、z轴,建立空间直角坐标系o﹣xyz,如图所示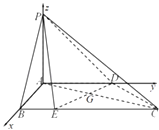
可得A(0,0,0)D(0,2,0),E(2,1,0),C(2,4,0),
P(0,0,λ) (λ>0)
∴ ![]() ,
, ![]() ,
, ![]()
得 ![]() ,
, ![]() ,
,
∴DE⊥AC且DE⊥AP,
∵AC、AP是平面PAC内的相交直线,∴ED⊥平面PAC.
∵ED平面PED∴平面PED⊥平面PAC
(Ⅱ)由(Ⅰ)得平面PAC的一个法向量是 ![]() ,
,![]()
设直线PE与平面PAC所成的角为θ,
则 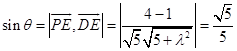 ,解之得λ=±2
,解之得λ=±2
∵λ>0,∴λ=2,可得P的坐标为(0,0,2)
设平面PCD的一个法向量为 ![]() =(x0 , y0 , z0),
=(x0 , y0 , z0), ![]() ,
, ![]()
由 ![]() ,
, ![]() ,得到
,得到 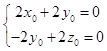 ,
,
令x0=1,可得y0=z0=﹣1,得 ![]() =(1,﹣1,﹣1)
=(1,﹣1,﹣1)
∴cos< ![]() ,
, ![]()
由图形可得二面角A﹣PC﹣D的平面角是锐角,
∴二面角A﹣PC﹣D的平面角的余弦值为 ![]() .
.
【解析】(I)由面面垂直的性质定理证出PA⊥平面ABCD,从而得到AB、AD、AP两两垂直,因此以AB、AD、AP为x轴、y轴、z轴,建立坐标系o﹣xyz,得A、D、E、C、P的坐标,进而得到 ![]() 、
、 ![]() 、
、 ![]() 的坐标.由数量积的坐标运算公式算出
的坐标.由数量积的坐标运算公式算出 ![]() 且
且 ![]() ,从而证出DE⊥AC且DE⊥AP,结合线面垂直判定定理证出ED⊥平面PAC,从而得到平面PED⊥平面PAC;(II)由(Ⅰ)得平面PAC的一个法向量是
,从而证出DE⊥AC且DE⊥AP,结合线面垂直判定定理证出ED⊥平面PAC,从而得到平面PED⊥平面PAC;(II)由(Ⅰ)得平面PAC的一个法向量是 ![]() ,算出
,算出 ![]() 、
、 ![]() 夹角的余弦,即可得到直线PE与平面PAC所成的角θ的正弦值,由此建立关于θ的方程并解之即可得到λ=2.利用垂直向量数量积为零的方法,建立方程组算出
夹角的余弦,即可得到直线PE与平面PAC所成的角θ的正弦值,由此建立关于θ的方程并解之即可得到λ=2.利用垂直向量数量积为零的方法,建立方程组算出 ![]() =(1,﹣1,﹣1)是平面平面PCD的一个法向量,结合平面PAC的法向量
=(1,﹣1,﹣1)是平面平面PCD的一个法向量,结合平面PAC的法向量 ![]() ,算出
,算出 ![]() 、
、 ![]() 的夹角余弦,再结合图形加以观察即可得到二面角A﹣PC﹣D的平面角的余弦值.
的夹角余弦,再结合图形加以观察即可得到二面角A﹣PC﹣D的平面角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的角
的角 所对的边份别为
所对的边份别为 ,且
,且
(1)求角
 的大小;
的大小;(2)若
 ,求
,求 的周长
的周长 的取值范围.
的取值范围. -
科目: 来源: 题型:
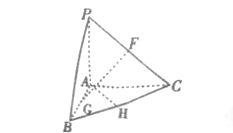
查看答案和解析>>【题目】如图,在三棱锥
 中,
中, 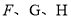 分别是
分别是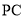 、
、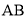 、
、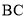 的中点,
的中点, 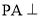 平面
平面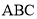 ,
, 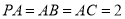 ,二面角
,二面角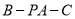 为
为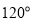 .
.
(1)证明:
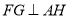 ;
;(2)求二面角
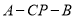 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
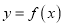 在实数集
在实数集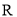 上的图象是连续不断的,且对任意实数
上的图象是连续不断的,且对任意实数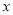 存在常数
存在常数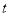 使得
使得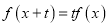 恒成立,则称
恒成立,则称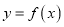 是一个“关于
是一个“关于 函数”.现有下列“关于
函数”.现有下列“关于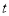 函数”的结论:
函数”的结论:①常数函数是“关于
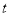 函数”;
函数”;②正比例函数必是一个“关于
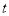 函数”;
函数”;③“关于
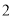 函数”至少有一个零点;
函数”至少有一个零点;④
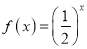 是一个“关于
是一个“关于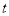 函数”.
函数”.其中正确结论的序号是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
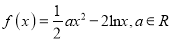 .
.(1)求函数
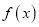 的单调区间;
的单调区间;(2)已知点
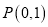 和函数
和函数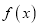 图像上动点
图像上动点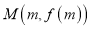 ,对任意
,对任意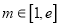 ,直线
,直线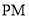 倾斜角都是钝角,求
倾斜角都是钝角,求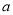 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某房地产开发公司计划在一楼区内建造一个长方形公园
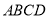 ,公园由长方形的休闲区
,公园由长方形的休闲区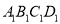 (阴影部分)和环公园人行道组成.已知休闲区
(阴影部分)和环公园人行道组成.已知休闲区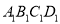 的面积为4000平方米,人行道的宽分别为4米和10米.
的面积为4000平方米,人行道的宽分别为4米和10米.(1)若设休闲区的长
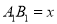 米,求公园
米,求公园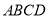 所占面积
所占面积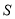 关于
关于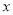 的函数
的函数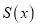 的解析式;
的解析式;(2)要使公园所占面积最小,休闲区
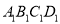 的长和宽该如何设计?
的长和宽该如何设计?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个抛物线型的拱桥,当水面离拱顶2 m时,水宽4 m,若水面下降1 m,求水的宽度.
相关试题

