【题目】已知函数![]() 的两个零点为
的两个零点为![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证: ![]() .
.
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析: (1)方法一的思路是:求出函数![]() 的最大值,有两个零点,再最大值一定大于零,求出实数
的最大值,有两个零点,再最大值一定大于零,求出实数![]() 的范围.方法二是转化为两个函数的图象有两个交点; (2)采用综合法和分析法证明不等式.构造函数
的范围.方法二是转化为两个函数的图象有两个交点; (2)采用综合法和分析法证明不等式.构造函数![]() ,利用单调性求出
,利用单调性求出![]() 的范围,构造函数
的范围,构造函数![]() ,证明
,证明![]() 在
在![]() 上为增函数,
上为增函数, ![]() ,化简,得证.
,化简,得证.
试题解析:(1)方法一: ![]() ,
,
①![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,不可能有两个零点.
上单调递增,不可能有两个零点.
②![]() 时,由
时,由![]() 可解得
可解得![]() ,由
,由![]() 可解得
可解得![]() .
.
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,于是
上单调递增,于是![]() .
.
要使得![]() 在
在![]() 上有两个零点,则
上有两个零点,则![]() ,解得
,解得![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
方法二: ![]() ,可转化为函数
,可转化为函数![]() 与函数
与函数![]() 图象有两个交点.
图象有两个交点.
∵![]() ,∴当
,∴当![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() .即
.即![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴![]() .
.
∴![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
(2)令![]() ,则
,则![]() ,由题意知方程
,由题意知方程![]() 有两个根
有两个根![]() ,即方程
,即方程![]() 有两个根
有两个根![]() ,不妨设
,不妨设![]() .
.
令![]() ,则
,则![]() ,由
,由![]() 可得
可得![]() ,由
,由![]() 可得
可得![]() ,∴
,∴![]() 时,
时, ![]() 单调递增,
单调递增, ![]() 时,
时, ![]() 单调递减.
单调递减.
根据已知有: ![]() ,要证
,要证![]() ,即证
,即证![]() ,即
,即![]() .
.
即证![]() .令
.令![]() ,下面证
,下面证![]() 对任意的
对任意的![]() 恒成立.
恒成立.
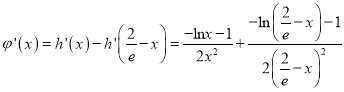 ,∵
,∵![]() ,∴
,∴![]() ,
, ![]() .
.
∴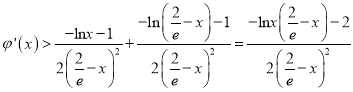 .
.
∵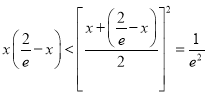 ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() 在
在![]() 是增函数,∴
是增函数,∴![]() ,∴
,∴![]() .
.
点睛: 本题主要考查函数的导数的综合应用,函数的单调性与零点,构造法的应用,考查学生分析问题解决问题的能力,难度比较大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过椭圆
 :
: 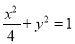 的左右焦点
的左右焦点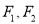 分别作直线
分别作直线 ,
,  交椭圆于
交椭圆于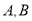 与
与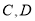 ,且
,且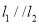 .
.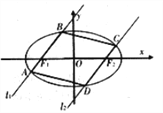
(1)求证:当直线
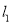 的斜率
的斜率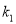 与直线
与直线 的斜率
的斜率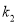 都存在时,
都存在时, 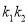 为定值;
为定值;(2)求四边形
 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|(a﹣1)x2﹣x+2=0}有且只有一个元素,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①已知集合M满足M{1,2,3},且M中至少有一个奇数,这样的集合M有6个;
②已知函数f(x)=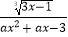 的定义域是R,则实数a的取值范围是(﹣12,0);
的定义域是R,则实数a的取值范围是(﹣12,0);
③函数f(x)=loga(x﹣3)+1(a>0且a≠1)图象恒过定点(4,2);
④已知函数f(x)=x2+bx+c对任意实数t都有f(3+t)=f(3﹣t),则f(1)>f(4)>f(3).
其中正确的命题序号是(写出所有正确命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】为评估设备
 生产某种零件的性能,从设备
生产某种零件的性能,从设备 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:直径/
58
59
61
62
63
64
65
66
67
68
69
70
71
73
合计
件数
1
1
3
5
6
19
33
18
4
4
2
1
2
1
100
经计算,样本的平均值
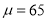 ,标准差
,标准差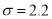 ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为
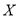 ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(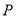 表示相应事件的概率);
表示相应事件的概率);①
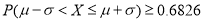 ;
;②
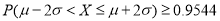 ;
;③
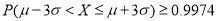
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备
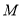 的性能等级.
的性能等级.(2)将直径小于等于
 或直径大于
或直径大于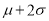 的零件认为是次品.
的零件认为是次品.①从设备
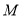 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数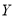 的数学期望
的数学期望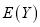 ;
;②从样本中随意抽取2件零件,计算其中次品个数
 的数学期望
的数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在多面体
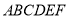 中,底面
中,底面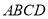 是边长为2的菱形,
是边长为2的菱形,  ,四边形
,四边形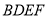 是矩形,平面
是矩形,平面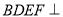 平面
平面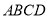 .
.(1)在图中画出过点
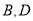 的平面
的平面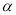 ,使得
,使得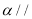 平面
平面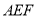 (必须说明画法,不需证明);
(必须说明画法,不需证明);(2)若二面角
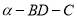 是
是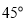 ,求
,求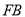 与平面
与平面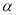 所成角的正弦值.
所成角的正弦值.
-
科目: 来源: 题型:
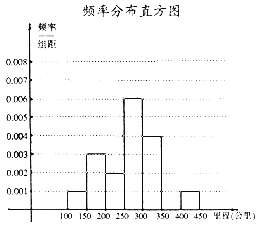
查看答案和解析>>【题目】面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.
频率分布表
分组
频数
频率
[100,150)
1
0.05
[150,200)
3
0.15
[200,250)
x
0.1
[250,300)
6
0.3
[300,350)
4
0.2
[350,400)
3
y
[400,450]
1
0.05
合计
N
1
(1)试确定频率分布表中x,y,N的值,并补全频率分布直方图;
(2)若从续航里程在[200,250)及[350,400)的车辆中随机抽取2辆车,求两辆车续航里程都在[350,400)的概率.
相关试题

