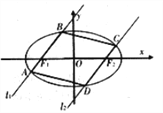
【题目】如图,过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() 分别作直线
分别作直线![]() ,
, ![]() 交椭圆于
交椭圆于![]() 与
与![]() ,且
,且![]() .
.
(1)求证:当直线![]() 的斜率
的斜率![]() 与直线
与直线![]() 的斜率
的斜率![]() 都存在时,
都存在时, ![]() 为定值;
为定值;
(2)求四边形![]() 面积的最大值.
面积的最大值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析: (1)设![]() ,分别将
,分别将![]() 坐标代入椭圆中,得出两等式,相减得出
坐标代入椭圆中,得出两等式,相减得出![]() ,写出
,写出![]() 的表达式,化简得出结果; (2)设直线
的表达式,化简得出结果; (2)设直线![]() 的方程
的方程![]() ,联立直线
,联立直线![]() 的方程和椭圆方程,求出
的方程和椭圆方程,求出![]() ,算出
,算出![]() 的表达式,而
的表达式,而![]() ,代入,用基本不等式求出最大值,再得出四边形
,代入,用基本不等式求出最大值,再得出四边形![]() 面积的最大值.
面积的最大值.
试题解析: (1)设![]() ,
, ![]() ,根据对称性,有
,根据对称性,有![]() ,因为
,因为![]() ,
, ![]() 都在椭圆
都在椭圆![]() 上,所以
上,所以![]() ,
, ![]() ,二式相减得,
,二式相减得, ![]() ,所以
,所以![]() 为定值.
为定值.
(2)当![]() 的倾斜角为
的倾斜角为![]() 时,
时, ![]() 与
与![]() 重合,舍去.
重合,舍去.
当![]() 的倾斜角不为0时,由对称性得四边形
的倾斜角不为0时,由对称性得四边形![]() 为平行四边形,
为平行四边形, ![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,得
,得![]() .显然
.显然![]() ,
, ![]() ,
, ![]() .
.
所以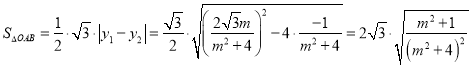
设![]() ,所以
,所以![]() ,
, ![]() .所以
.所以 .
.
当且仅当![]() 即
即![]() 时等号成立,所以
时等号成立,所以![]() .
.
所以平行四边形面积的最大值为![]() .
.
点睛: 本题主要考查直线与椭圆相交时的有关知识,考查学生分析问题解决问题的能力,属于中档题.解题技巧: 在(1)中,采用设而不求;在(2)中, 设直线![]() 的方程
的方程![]() 比
比![]() 好,因为联立直线与椭圆方程计算量减少,还有
好,因为联立直线与椭圆方程计算量减少,还有![]() ,由韦达定理可求出
,由韦达定理可求出![]() .在求三角形
.在求三角形![]() 面积最大值时,将
面积最大值时,将![]() 看成一个整体,利用基本不等式求出最大值.
看成一个整体,利用基本不等式求出最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
 中,
中, 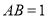 ,
, 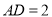 ,点
,点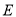 为
为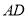 中点,沿
中点,沿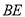 将
将 折起至
折起至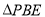 ,如下图所示,点
,如下图所示,点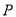 在面
在面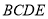 的射影
的射影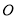 落在
落在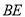 上.
上.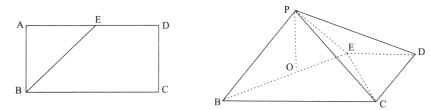
(Ⅰ)求证:
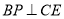 ;
;(Ⅱ)求二面角
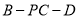 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)=
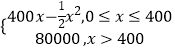 ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划面向高一年级
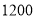 名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了
名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了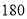 名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有
名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有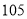 人.在这
人.在这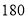 名学生中选择社会科学类的男生、女生均为
名学生中选择社会科学类的男生、女生均为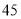 人.
人.(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的
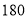 名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过
名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过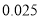 的前提下认为科类的选择与性别有关?
的前提下认为科类的选择与性别有关?选择自然科学类
选择社会科学类
合计
男生
女生
合计
附:
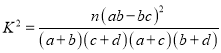 ,其中
,其中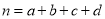 .
.
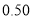

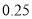
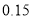
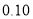
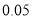
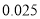

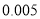
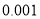


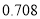
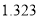
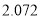
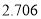
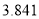
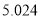
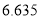
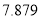
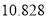
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|(a﹣1)x2﹣x+2=0}有且只有一个元素,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①已知集合M满足M{1,2,3},且M中至少有一个奇数,这样的集合M有6个;
②已知函数f(x)=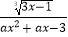 的定义域是R,则实数a的取值范围是(﹣12,0);
的定义域是R,则实数a的取值范围是(﹣12,0);
③函数f(x)=loga(x﹣3)+1(a>0且a≠1)图象恒过定点(4,2);
④已知函数f(x)=x2+bx+c对任意实数t都有f(3+t)=f(3﹣t),则f(1)>f(4)>f(3).
其中正确的命题序号是(写出所有正确命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
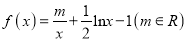 的两个零点为
的两个零点为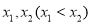 .
.(1)求实数
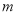 的取值范围;
的取值范围;(2)求证:
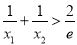 .
.
相关试题

