《2025年成才之路高中新课程学习指导高中数学选择性必修第三册人教版》

1. 从$A$ 地到$B$ 地，可乘汽车、火车、轮船三种交通工具，如果一天内汽车发3 次，火车发4 次，轮船发2 次，那么一天内乘坐这三种交通工具的不同走法数为
(B)

A.3
B.9
C.24
D.以上都不对

答案： 1.B 根据分类加法计数原理可得，一天内乘坐这三种交通工具的不同走法数为3+4+2=9.

2. 从集合$\{0, 1, 2, 3, 4, 5, 6\}$ 中任取两个互不相等的数$a$, $b$ 组成复数$a + bi$，其中纯虚数的个数为
(C)

A.0
B.3
C.6
D.36

答案： 2.C 由复数a+bi为纯虚数，所以a=0，此时b有6种取法，故纯虚数共有6个.

3. 阅读课上，5 名同学分别从3 种不同的书中选择一种进行阅读，不同的选法种数是 (D)

A.50
B.60
C.125
D.243

答案： 3.D 由题意，5名同学分别从3种不同的书中选择一种进行阅读，其中，每名同学都有3种不同的选法，所以不同的选法种数是$3^{5} =243$.故选D.

4. 某班小张等4 名同学报名参加$A$, $B$, $C$ 三个课外活动小组，每名同学限报其中一个小组，且小张不能报$A$ 小组，则不同的报名方法有
(C)

A.27 种
B.36 种
C.54 种
D.81 种

答案： 4.C 小张的报名方法有2种，其他3名同学的报名方法各有3种，由分步乘法计数原理知，共有2×3×3×3=54(种)不同的报名方法，故选C.

5. (多选)已知$a \in \{1, 2, 3\}$，$b \in \{4, 5, 6, 7\}$，$r \in \{8, 9\}$，则方程$(x - a)^2 + (y - b)^2 = r^2$ 可表示不同的圆的个数用式子表示为
(AD)

A.$4 + 4 + 4 + 4 + 4 + 4$
B.$4 + 4 + 4 + 4$
C.$3 × 4$
D.$3 × 4 × 2$

答案： 5.AD 方法一：完成表示不同的圆这件事有三步：第1步，确定a有3种不同的取法；第2步，确定b有4种不同的取法；第3步，确定r有2种不同的取法.由分步乘法计数原理，方程$(x - a)^ {2} + (y - b)^ {2} = r^ {2}$可表示不同的圆共有3×4×2(个).
方法二：由分类加法计数原理得，当a=1时，b=4,5,6,7，r=8或9，有4+4(个)；当a=2时，b=4,5,6,7，r=8或9，有4+4(个)；当a=3时，b=4,5,6,7，r=8或9，有4+4(个)，故方程$(x - a)^ {2} + (y - b)^ {2} = r^ {2}$可表示不同的圆共有4+4+4+4+4+4(个).

6. (多选)设东、西、南、北四面通往山顶的路各有2, 3, 3, 4 条，只从一面上山，而从其他任意一面下山，不同的走法种数可能为 (ABC)

A.20
B.27
C.32
D.30

答案： 6.ABC 东面上山的种数为2×(3+3+4)=20，西面上山的种数为3×(2+3+4)=27，南面上山的种数为3×(2+3+4)=27，北面上山的种数为4×(2+3)=32，故只从一面上山，而从其他任意一面下山的走法种数可能为20,27,32.

7. 某学生去书店，发现3 本好书，决定至少买其中1 本，则购买方式共有7种.

答案： 7.7 分3类：买1本书，买2本书和买3本书.各类的购买方式依次有3种、3种和1种，故购买方式共有3+3+1=7(种).

8. 已知两条异面直线$a$, $b$ 上分别有4 个点和7 个点，则这11 个点可以确定不同的平面个数
为11.

答案： 8.11 依据直线和直线外一点确定一个平面，分两类情况讨论：第1类，直线a分别与直线b上的7个点可以确定7个不同的平面；第2类，直线b分别与直线a上的4个点可以确定4个不同的平面.根据分类加法计数原理知，共可以确定7+4=11个不同的平面.

9. 甲、乙、丙3 个班各有3 名、5 名、2 名三好学生，现准备推选2 名来自不同班的三好学生去参加校三好学生代表大会，共有31种推选方法.

答案： 9.31 分为三类：①甲班选1名，乙班选1名，根据分步乘法计数原理，有3×5=15(种)选法；②甲班选1名，丙班选1名，根据分步乘法计数原理，有3×2=6(种)选法；③乙班选1名，丙班选1名，根据分步乘法计数原理，有5×2=10(种)选法.
综上，根据分类加法计数原理，共有15+6+10=31(种)推选方法.

10. 设集合$A = \{1, 2, 3, 4\}$，$m, n \in A$，则方程$\frac{x^2}{m} + \frac{y^2}{n} = 1$ 表示焦点位于$x$ 轴上的椭圆有多少个?

答案： 10.【解析】 因为椭圆的焦点位于x轴上，所以$m＞n$.
当$m=4$时，$n=1,2,3$；
当$m=3$时，$n=1,2$；
当$m=2$时，$n=1$.
所求的椭圆共有3+2+1=6(个).

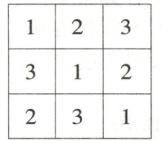
11. 将1, 2, 3 填入$3 × 3$ 的方格格中，要求每行、每列都没有重复数字，如图是一种填法，则不同的填写方法共有
(B)


A.6 种
B.12 种
C.24 种
D.48 种

答案： 11.B 假设第一行为1,2,3，则第二行第一列可为2或3，此时其他剩余的空格都只有一种填法，又第一行有$3×2×1=6$(种)填法.故不同的填写方法共有$6×2=12$(种).

12. 某艺术小组有9 人，每人至少会钢琴和小号中的一种，其中7 人会钢琴，3 人会小号，从中选出会钢琴与会小号的各1 人，则有20种不同的选法.

答案： 20 由题意可知，有1人既会钢琴又会小号(记为甲)，只会钢琴的有6人，只会小号的有2人.本题可分两类：第1类，甲入选，此时，只需从其他8人中任选1人，故这类选法共有
种.第2类，甲不入选，此时，选法共有$6×2=12$(种).因此有8+12=20(种)不同的选法.

13. 设$a$, $b$, $c \in \{1, 2, 3, 4\}$，若以$a$, $b$, $c$ 为三条边的长构成一个等腰三角形，则这样的三角形有12个.

答案： 13.12 设a,b是腰长，根据腰长分四类：第1类，当a=b=c＜a+b=2，则c=1；第2类，当a=b=2时，c＜a+b=4，=1,2,3；第3类，当a=b=3时，c＜a+b=6，则c=1,2,.
第4类，当a=b=4时，c＜a+b=8，则c=1,2,3,4.因此个条件的三角形的个数为1+3+4+4=12.

14. 用1, 2, 3, 4 四个数字(可重复)排成三位数，并把这些三位数由小到大排成一个数列$\{a_n\}$.
(1) 写出这个数列的前11 项；
(2) 这个数列共有多少项?
(3) 若$a_n = 341$，求$n$.

答案：
14.【解析】
(1)111,112,113,114,121,122,123,124,131,132,133.
(2)这个数列的项数就是用1,2,3,4排成的三位数的个数，每个数位上都有4种排法，则共有$4×4×4=64$(项).
(3)比$a_{n} =341$小的数有两类：
①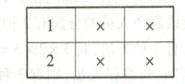
②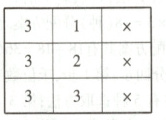
共有$2×4×4+1×3×4=44$(项).
所以n=44+1=45.