2025年一遍过三年级数学上册西南大学版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一遍过三年级数学上册西南大学版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1 想一想,填一填。

(1)
(2)把一条线段向两端无限延伸,就形成了一条( );把一条线段向一个方向无限延伸,就形成了一条( )。

(1)
(2)把一条线段向两端无限延伸,就形成了一条( );把一条线段向一个方向无限延伸,就形成了一条( )。
答案:
1
(1)
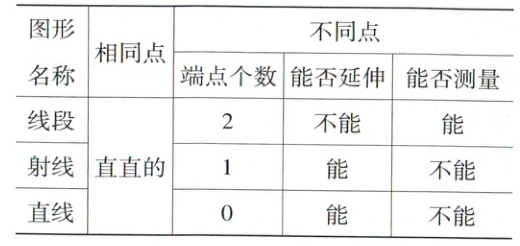
(2)直线、射线
1
(1)

(2)直线、射线
2 如图,在一条直线上有 $ A、B、C、D $ 四个点。

(1)以点 $ B $ 为一个端点的线段有(
(2)以点 $ B $ 为一个端点的射线有(

(1)以点 $ B $ 为一个端点的线段有(
3
)条,分别是(线段BA、线段BC、线段BD
)。(2)以点 $ B $ 为一个端点的射线有(
2
)条,分别是(射线BA、射线BC(或射线BD)
)。
答案:
2
(1)3 线段BA、线段BC、线段BD
(2)2 射线BA、射线BC(或射线BD)
(1)3 线段BA、线段BC、线段BD
(2)2 射线BA、射线BC(或射线BD)
3 (教材 P92 第 3 题变设问)按要求做一做。

(1)过点 $ A $ 画直线 $ l $。我发现经过一个点可以画(
(2)过 $ B、C $ 两点画直线 $ BC $。我发现经过两个点可以画(
(3)在直线 $ BC $ 上取一个点 $ D $,使线段 $ CD $ 长为 $ 2 cm $。
(4)画出射线 $ CA $。
(5)数一数,画好的图形中有(

(1)过点 $ A $ 画直线 $ l $。我发现经过一个点可以画(
无数
)条直线。(2)过 $ B、C $ 两点画直线 $ BC $。我发现经过两个点可以画(
1
)条直线。(3)在直线 $ BC $ 上取一个点 $ D $,使线段 $ CD $ 长为 $ 2 cm $。
(4)画出射线 $ CA $。
(5)数一数,画好的图形中有(
2
)条直线,(10
)条射线,(4
)条线段。
答案:
3

(1)画图如上,画法不唯一,无数
(2)画图如上,1
(3)画图如上,画法不唯一,可以在点C左侧,也可以在点C右侧
(4)画图如上
(5)2,10,4
3

(1)画图如上,画法不唯一,无数
(2)画图如上,1
(3)画图如上,画法不唯一,可以在点C左侧,也可以在点C右侧
(4)画图如上
(5)2,10,4
4 (探究题·规律探究)观察前两个图中数线段的方法,数一数、填一填,然后用同样的方法数出第 3 个图中的线段条数。

(

(
3
)条 (6
)条 (15
)条
答案:
4
3,6

15
解析:观察给出的前两个图。

3个端点,从左边第1个端点引出①②2条线段,从左边第2个端点引出③1条线段,共2 + 1 = 3(条)线段。

4个端点,从左边第1个端点引出①②③3条线段,从左边第2个端点引出④⑤2条线段,从左边第3个端点引出⑥1条线段,共3 + 2 + 1 = 6(条)线段。
发现数线段的方法是按顺序依次数。也发现存在下面的规律:
有几个端点,就有(几 - 1)+(几 - 2)+…+1条线段。
4
3,6

15
解析:观察给出的前两个图。

3个端点,从左边第1个端点引出①②2条线段,从左边第2个端点引出③1条线段,共2 + 1 = 3(条)线段。

4个端点,从左边第1个端点引出①②③3条线段,从左边第2个端点引出④⑤2条线段,从左边第3个端点引出⑥1条线段,共3 + 2 + 1 = 6(条)线段。
发现数线段的方法是按顺序依次数。也发现存在下面的规律:
有几个端点,就有(几 - 1)+(几 - 2)+…+1条线段。
查看更多完整答案,请扫码查看


