2026年理想树试题攻略高中数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年理想树试题攻略高中数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
11. 已知函数 $ f(x) = \frac{1}{2}x^2 + 4x - (4x + 1)\ln x $,则下列结论中正确的是(
A.$ f(x) $ 有四个单调区间
B.$ f(x) $ 存在最小值
C.$ f(x) $ 有三个极值点,从小到大依次为 $ a $,$ b $,$ c $,则 $ a $,$ b $,$ c $ 成等差数列
D.$ f(x) $ 有三个极值点,从小到大依次为 $ a $,$ b $,$ c $,则 $ a $,$ b $,$ c $ 成等比数列
ABD
)A.$ f(x) $ 有四个单调区间
B.$ f(x) $ 存在最小值
C.$ f(x) $ 有三个极值点,从小到大依次为 $ a $,$ b $,$ c $,则 $ a $,$ b $,$ c $ 成等差数列
D.$ f(x) $ 有三个极值点,从小到大依次为 $ a $,$ b $,$ c $,则 $ a $,$ b $,$ c $ 成等比数列
答案:
11.ABD新趋考点利用导数求函数的单调区间、极值与最值,等比数列的判断
思路导引$f(x)\rightarrow f^{\prime}(x)=x - 4\ln x - \frac{1}{x}$ 令$g(x)=f^{\prime}(x)$,$g^{\prime}(x)=\frac{x^{2}-4x + 1}{x^{2}}\rightarrow g(x)$的单调性$\rightarrow f^{\prime}(x)$的单调性,$f^{\prime}(\frac{1}{e^{3}})<0,f^{\prime}(1)=0$,$\rightarrow$存在$a\in(\frac{1}{e^{3}},2-\sqrt{3})$,$c\in(2+\sqrt{3},e^{3})$使$f^{\prime}(a)=f^{\prime}(c)=0\rightarrow f(x)$的单调区间和最小值$\rightarrow$A,B正确;$f^{\prime}(\frac{1}{x})=-f^{\prime}(x)\rightarrow f^{\prime}(a)=-f^{\prime}(c)=0\rightarrow a = \frac{1}{c}$,$a,1,c$为$f(x)$的三个极值点$\rightarrow ac = 1\rightarrow a,1,c$成等比数列$\rightarrow$C错误,D正确。
[深度解析]对于A,B,由题可得,函数$f(x)$的定义域为$(0, + \infty)$,$f^{\prime}(x)=x - 4\ln x - \frac{4x + 1}{x}=x - 4\ln x - \frac{1}{x}$。令$g(x)=x - 4\ln x - \frac{1}{x}(x>0)$,则$g^{\prime}(x)=\frac{x^{2}-4x + 1}{x^{2}}$,令$g^{\prime}(x)=0$,解得$x = 2-\sqrt{3}$或$x = 2+\sqrt{3}$。当$x\in(0,2-\sqrt{3})$时,$g^{\prime}(x)>0$,$g(x)$单调递增;当$x\in(2-\sqrt{3},2+\sqrt{3})$时,$g^{\prime}(x)<0$,$g(x)$单调递减;当$x\in(2+\sqrt{3}, + \infty)$时,$g^{\prime}(x)>0$,$g(x)$单调递增。又$f^{\prime}(\frac{1}{e^{3}})=\frac{1}{e^{3}}-4\ln\frac{1}{e^{3}}-\frac{1}{\frac{1}{e^{3}}}=e^{3}+\frac{1}{e^{3}}-12<0$,$f^{\prime}(1)=0$,$f^{\prime}(e^{3})>0$,所以存在$a\in(\frac{1}{e^{3}},2-\sqrt{3})$,$c\in(2+\sqrt{3},e^{3})$,使得$f^{\prime}(a)=f^{\prime}(c)=0$(提示:已知函数的二阶导数,利用该信息判断一阶导数的取值情况,主要是判断其正负,但是由于导函数形式较为复杂,所以可以利用卡根法确定其零点所在的区间),故$x\in(0,a)\cup(1,c)$时,$f^{\prime}(x)<0$,$x\in(a,1)\cup(c, + \infty)$时,$f^{\prime}(x)>0$,所以函数$f(x)$在$(0,a)$,$(1,c)$上单调递减,在$(a,1)$,$(c, + \infty)$上单调递增,故$f(x)$有四个单调区间,且存在最小值,最小值为$\min\{f(a),f(c)\}$,故A,B正确。
对于C,D,由A,B分析知$f(x)$存在三个极值点$a$,$1$,$c$,因为$f^{\prime}(\frac{1}{x})=\frac{1}{x}-4\ln\frac{1}{x}-x=-f^{\prime}(x)$(关键:得到$f^{\prime}(x)$的性质,即$f^{\prime}(\frac{1}{x})=-f^{\prime}(x)$),又$f^{\prime}(a)=-f^{\prime}(c)=0$,所以$a = \frac{1}{c}$,即$ac = 1$,所以$a$,$1$,$c$成等比数列,故C错误,D正确。故选ABD。
思路导引$f(x)\rightarrow f^{\prime}(x)=x - 4\ln x - \frac{1}{x}$ 令$g(x)=f^{\prime}(x)$,$g^{\prime}(x)=\frac{x^{2}-4x + 1}{x^{2}}\rightarrow g(x)$的单调性$\rightarrow f^{\prime}(x)$的单调性,$f^{\prime}(\frac{1}{e^{3}})<0,f^{\prime}(1)=0$,$\rightarrow$存在$a\in(\frac{1}{e^{3}},2-\sqrt{3})$,$c\in(2+\sqrt{3},e^{3})$使$f^{\prime}(a)=f^{\prime}(c)=0\rightarrow f(x)$的单调区间和最小值$\rightarrow$A,B正确;$f^{\prime}(\frac{1}{x})=-f^{\prime}(x)\rightarrow f^{\prime}(a)=-f^{\prime}(c)=0\rightarrow a = \frac{1}{c}$,$a,1,c$为$f(x)$的三个极值点$\rightarrow ac = 1\rightarrow a,1,c$成等比数列$\rightarrow$C错误,D正确。
[深度解析]对于A,B,由题可得,函数$f(x)$的定义域为$(0, + \infty)$,$f^{\prime}(x)=x - 4\ln x - \frac{4x + 1}{x}=x - 4\ln x - \frac{1}{x}$。令$g(x)=x - 4\ln x - \frac{1}{x}(x>0)$,则$g^{\prime}(x)=\frac{x^{2}-4x + 1}{x^{2}}$,令$g^{\prime}(x)=0$,解得$x = 2-\sqrt{3}$或$x = 2+\sqrt{3}$。当$x\in(0,2-\sqrt{3})$时,$g^{\prime}(x)>0$,$g(x)$单调递增;当$x\in(2-\sqrt{3},2+\sqrt{3})$时,$g^{\prime}(x)<0$,$g(x)$单调递减;当$x\in(2+\sqrt{3}, + \infty)$时,$g^{\prime}(x)>0$,$g(x)$单调递增。又$f^{\prime}(\frac{1}{e^{3}})=\frac{1}{e^{3}}-4\ln\frac{1}{e^{3}}-\frac{1}{\frac{1}{e^{3}}}=e^{3}+\frac{1}{e^{3}}-12<0$,$f^{\prime}(1)=0$,$f^{\prime}(e^{3})>0$,所以存在$a\in(\frac{1}{e^{3}},2-\sqrt{3})$,$c\in(2+\sqrt{3},e^{3})$,使得$f^{\prime}(a)=f^{\prime}(c)=0$(提示:已知函数的二阶导数,利用该信息判断一阶导数的取值情况,主要是判断其正负,但是由于导函数形式较为复杂,所以可以利用卡根法确定其零点所在的区间),故$x\in(0,a)\cup(1,c)$时,$f^{\prime}(x)<0$,$x\in(a,1)\cup(c, + \infty)$时,$f^{\prime}(x)>0$,所以函数$f(x)$在$(0,a)$,$(1,c)$上单调递减,在$(a,1)$,$(c, + \infty)$上单调递增,故$f(x)$有四个单调区间,且存在最小值,最小值为$\min\{f(a),f(c)\}$,故A,B正确。
对于C,D,由A,B分析知$f(x)$存在三个极值点$a$,$1$,$c$,因为$f^{\prime}(\frac{1}{x})=\frac{1}{x}-4\ln\frac{1}{x}-x=-f^{\prime}(x)$(关键:得到$f^{\prime}(x)$的性质,即$f^{\prime}(\frac{1}{x})=-f^{\prime}(x)$),又$f^{\prime}(a)=-f^{\prime}(c)=0$,所以$a = \frac{1}{c}$,即$ac = 1$,所以$a$,$1$,$c$成等比数列,故C错误,D正确。故选ABD。
12. 已知数列 $ \{ a_n \} $ 是等差数列,若 $ a_1 + a_3 + a_5 = 105 $,$ a_6 = 41 $,则数列 $ \{ a_n \} $ 的公差 $ d = $
2
。
答案:
12.2基础考点等差数列的通项公式、等差数列的性质
[深度解析](基本量法)由题知,$\begin{cases}a_{1}+a_{3}+a_{5}=3a_{1}+6d=105\\a_{6}=a_{1}+5d=41\end{cases}$,解得$d = 2$。
二题多解(等差中项法)由$a_{1}+a_{3}+a_{5}=105$,解得$3a_{3}=105$,所以$a_{3}=35$,又$a_{6}=41$,所以$d=\frac{a_{6}-a_{3}}{3}=2$。
[深度解析](基本量法)由题知,$\begin{cases}a_{1}+a_{3}+a_{5}=3a_{1}+6d=105\\a_{6}=a_{1}+5d=41\end{cases}$,解得$d = 2$。
二题多解(等差中项法)由$a_{1}+a_{3}+a_{5}=105$,解得$3a_{3}=105$,所以$a_{3}=35$,又$a_{6}=41$,所以$d=\frac{a_{6}-a_{3}}{3}=2$。
13. 若直线 $ l: x - 2y + m = 0 (m \neq 0) $ 被圆 $ C: (x + 1)^2 + (y - 2)^2 = 8 $ 截得的弦长为 $ 2\sqrt{3} $,则 $ m = $
10
。
答案:
13.10热门考点直线与圆的位置关系、点到直线的距离公式、圆的弦长公式
[深度解析]由题可得,圆$C$:$(x + 1)^{2}+(y - 2)^{2}=8$的圆心为$C(-1,2)$,半径$r = 2\sqrt{2}$。设圆心到直线$l$的距离为$d$,由弦长公式可得$2\sqrt{r^{2}-d^{2}}=2\sqrt{3}$,解得$d = \sqrt{5}$,所以圆心$(-1,2)$到直线$l:x - 2y + m = 0$的距离$d=\frac{|-5 + m|}{\sqrt{5}}=\sqrt{5}$,解得$m = 0$或$m = 10$,又$m\neq0$,所以$m = 10$。
[深度解析]由题可得,圆$C$:$(x + 1)^{2}+(y - 2)^{2}=8$的圆心为$C(-1,2)$,半径$r = 2\sqrt{2}$。设圆心到直线$l$的距离为$d$,由弦长公式可得$2\sqrt{r^{2}-d^{2}}=2\sqrt{3}$,解得$d = \sqrt{5}$,所以圆心$(-1,2)$到直线$l:x - 2y + m = 0$的距离$d=\frac{|-5 + m|}{\sqrt{5}}=\sqrt{5}$,解得$m = 0$或$m = 10$,又$m\neq0$,所以$m = 10$。
14. 一个 $ 3 × 3 $ 的正方形花坛被划分为 9 个 $ 1 × 1 $ 小方格(如图),计划种植 4 种花卉(玫瑰、月季、百合、郁金香),每个小方格种 1 种花卉。要求:花坛中任意 $ 2 × 2 $ 的小区域内,4 种花卉必须全部种植且不重复,则不同的种植方法共有

72
种。
答案:
14.72重难考点计数原理的应用
思路导引对正方形每个方格编号$\rightarrow$先种植$1,2,4,5$方格,有$A_{4}^{4}$种不同的种植方法$\rightarrow$
$\begin{cases}当6方格种植A花卉时\rightarrow剩余方格有1种种植方法\\当6方格种植D花卉时\rightarrow讨论9方格种植A或B花卉\end{cases}\rightarrow$共有$24×(1 + 1 + 1)=72$种不同的种植方法
[深度解析]如图①,对正方形每个方格编号,记玫瑰、月季、百合、郁金香分别为$A,B,C,D$。 第一步:在$1,2,4,5$方格中种植4种不同花卉,有$A_{4}^{4}=24$(种)方法。第二步:不妨取1种种植情况如图②。
第一步:在$1,2,4,5$方格中种植4种不同花卉,有$A_{4}^{4}=24$(种)方法。第二步:不妨取1种种植情况如图②。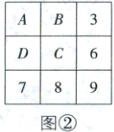
(1)当6方格种植$A$花卉时,$3$方格只能种植$D$花卉,$8$格种植$B$花卉,$7$方格种植$A$花卉,$9$方格种植$D$花卉,只有1种方法。
(2)当6方格不种植$A$花卉时,则6方格种植$D$花卉,$3$方格只能种植$A$花卉,
①当9方格种植$A$花卉时,$8$方格只能种植$B$花卉,$7$方格种植$A$花卉,只有1种方法;
②当9方格种植$B$花卉时,$8$方格只能种植$A$花卉,$7$方格种植$B$花卉,只有1种方法。
因此根据分类加法计数原理和分步乘法计数原理可知,共有$24×(1 + 1 + 1)=72$(种)不同的种植方法。
关键点拨在左上角的$2×2$小区域内填上$A,B,C,D$后,需要讨论6方格种植$A$花卉或种植$D$花卉时,剩下的方格有几种不同的种植方法。
14.72重难考点计数原理的应用
思路导引对正方形每个方格编号$\rightarrow$先种植$1,2,4,5$方格,有$A_{4}^{4}$种不同的种植方法$\rightarrow$
$\begin{cases}当6方格种植A花卉时\rightarrow剩余方格有1种种植方法\\当6方格种植D花卉时\rightarrow讨论9方格种植A或B花卉\end{cases}\rightarrow$共有$24×(1 + 1 + 1)=72$种不同的种植方法
[深度解析]如图①,对正方形每个方格编号,记玫瑰、月季、百合、郁金香分别为$A,B,C,D$。
 第一步:在$1,2,4,5$方格中种植4种不同花卉,有$A_{4}^{4}=24$(种)方法。第二步:不妨取1种种植情况如图②。
第一步:在$1,2,4,5$方格中种植4种不同花卉,有$A_{4}^{4}=24$(种)方法。第二步:不妨取1种种植情况如图②。
(1)当6方格种植$A$花卉时,$3$方格只能种植$D$花卉,$8$格种植$B$花卉,$7$方格种植$A$花卉,$9$方格种植$D$花卉,只有1种方法。
(2)当6方格不种植$A$花卉时,则6方格种植$D$花卉,$3$方格只能种植$A$花卉,
①当9方格种植$A$花卉时,$8$方格只能种植$B$花卉,$7$方格种植$A$花卉,只有1种方法;
②当9方格种植$B$花卉时,$8$方格只能种植$A$花卉,$7$方格种植$B$花卉,只有1种方法。
因此根据分类加法计数原理和分步乘法计数原理可知,共有$24×(1 + 1 + 1)=72$(种)不同的种植方法。
关键点拨在左上角的$2×2$小区域内填上$A,B,C,D$后,需要讨论6方格种植$A$花卉或种植$D$花卉时,剩下的方格有几种不同的种植方法。
15.(13 分)
已知函数 $ f(x) = \cos(\omega x + \varphi) (\omega > 0, |\varphi| < \frac{\pi}{2}) $ 的最小正周期是 $ \pi $,且满足 $ f(\frac{\pi}{6}) = \frac{\sqrt{3}}{2} $。
(1) 求函数 $ f(x) $ 的解析式;
(2) 设函数 $ g(x) = f(x + \frac{\pi}{12}) + \sqrt{3}f(x - \frac{\pi}{6}) $,求 $ g(x) $ 在区间 $ [-\frac{\pi}{4}, \frac{\pi}{4}] $ 上的最大值和最小值。
已知函数 $ f(x) = \cos(\omega x + \varphi) (\omega > 0, |\varphi| < \frac{\pi}{2}) $ 的最小正周期是 $ \pi $,且满足 $ f(\frac{\pi}{6}) = \frac{\sqrt{3}}{2} $。
(1) 求函数 $ f(x) $ 的解析式;
(2) 设函数 $ g(x) = f(x + \frac{\pi}{12}) + \sqrt{3}f(x - \frac{\pi}{6}) $,求 $ g(x) $ 在区间 $ [-\frac{\pi}{4}, \frac{\pi}{4}] $ 上的最大值和最小值。
答案:
15.经典题型正弦型、余弦型函数的性质、两角和的正弦公式
[解]
(1)第一步:根据周期公式求$\omega$的值
$\because f(x)=\cos(\omega x+\varphi)(\omega>0)$的最小正周期$T$为$\pi$,
$\therefore T=\frac{2\pi}{\omega}=\pi$,解得$\omega = 2$,$\therefore f(x)=\cos(2x+\varphi)$。……2分
第二步:根据所给函数值求$\varphi$的值
$\because f(\frac{\pi}{6})=\frac{\sqrt{3}}{2}$,$\therefore\cos(\frac{\pi}{3}+\varphi)=\frac{\sqrt{3}}{2}$,
$\therefore\frac{\pi}{3}+\varphi=\pm\frac{\pi}{6}+2k\pi$,$k\in\mathbf{Z}$,$\therefore\varphi=-\frac{\pi}{6}+2k\pi$或$\varphi=-\frac{\pi}{2}+2k\pi$,$k\in\mathbf{Z}$。$\because|\varphi|<\frac{\pi}{2}$,$\therefore\varphi=-\frac{\pi}{6}$。……4分
第三步:写出函数解析式
$\therefore f(x)=\cos(2x-\frac{\pi}{6})$。……6分
(2)第一步:求函数$g(x)$的解析式并利用两角和的正弦公式化简
$g(x)=f(x+\frac{\pi}{12})+\sqrt{3}f(x-\frac{\pi}{6})=\cos[2(x+\frac{\pi}{12})-\frac{\pi}{6}]+\sqrt{3}\cos[2(x-\frac{\pi}{6})-\frac{\pi}{6}]=\cos2x+\sqrt{3}\cos[2x-\frac{\pi}{2}-\frac{\pi}{6}]=2(\frac{1}{2}\cos2x+\frac{\sqrt{3}}{2}\sin2x)=2\sin(2x+\frac{\pi}{6})$(题眼)。……9分
第二步:令$\theta = 2x+\frac{\pi}{6}$,根据给定区间判断函数$y = 2\sin\theta$的单调性
令$\theta = 2x+\frac{\pi}{6}$,由$x\in[-\frac{\pi}{4},\frac{\pi}{4}]$,得$\theta\in[-\frac{\pi}{3},\frac{2\pi}{3}]$。
$\therefore y = 2\sin\theta$在$[-\frac{\pi}{3},\frac{\pi}{2}]$上单调递增,在$[\frac{\pi}{2},\frac{2\pi}{3}]$上单调递减。……10分
第三步:求函数$g(x)$的最值
$\therefore$当$2x+\frac{\pi}{6}=\frac{\pi}{2}$,即$x=\frac{\pi}{6}$时,$\sin(2x+\frac{\pi}{6})=1$,$g(x)$取得最大值,最大值为2。
当$2x+\frac{\pi}{6}=-\frac{\pi}{3}$,即$x=-\frac{\pi}{4}$时,$\sin(2x+\frac{\pi}{6})=-\frac{\sqrt{3}}{2}$,$g(-\frac{\pi}{4})=2×(-\frac{\sqrt{3}}{2})=-\sqrt{3}$,
当$2x+\frac{\pi}{6}=\frac{2\pi}{3}$,即$x=\frac{\pi}{4}$时,$\sin(2x+\frac{\pi}{6})=\frac{\sqrt{3}}{2}$,$g(\frac{\pi}{4})=2×\frac{\sqrt{3}}{2}=\sqrt{3}$(提示:在求函数在闭区间上的最值时,注意端点值的比较)。……11分
$\therefore g(x)$在区间$[-\frac{\pi}{4},\frac{\pi}{4}]$上的最大值为2,最小值为$-\sqrt{3}$。……13分
一两角题差多的解余弦(公2)式第化一简步:求函数$g(x)$的解析式并利用
$\because g(x)=f(x+\frac{\pi}{12})+\sqrt{3}f(x-\frac{\pi}{6})=\cos[2(x+\frac{\pi}{12})-\frac{\pi}{6}]+\sqrt{3}\cos[2(x-\frac{\pi}{6})-\frac{\pi}{6}]=2(\frac{1}{2}\cos2x+\frac{\sqrt{3}}{2}\sin2x)=2\cos(2x-\frac{\pi}{3})$。……9分
第二步;令$t = 2x-\frac{\pi}{3}$,根据给定区间判断函数$y = 2\cos t$的单调性
令$t = 2x-\frac{\pi}{3}$,由$x\in[-\frac{\pi}{4},\frac{\pi}{4}]$,得$t\in[-\frac{5\pi}{6},\frac{\pi}{6}]$。
$\therefore y = 2\cos t$在$[-\frac{5\pi}{6},0]$上单调递增,在$[0,\frac{\pi}{6}]$上单调递减。……10分
第三步:求函数$g(x)$的最值
又$2\cos(-\frac{5\pi}{6})=-\sqrt{3}$,$2\cos0 = 2$,$2\cos\frac{\pi}{6}=\sqrt{3}$。……11分
$\therefore g(x)$在区间$[-\frac{\pi}{4},\frac{\pi}{4}]$上的最大值为2,最小值为$-\sqrt{3}$。……13分
[解]
(1)第一步:根据周期公式求$\omega$的值
$\because f(x)=\cos(\omega x+\varphi)(\omega>0)$的最小正周期$T$为$\pi$,
$\therefore T=\frac{2\pi}{\omega}=\pi$,解得$\omega = 2$,$\therefore f(x)=\cos(2x+\varphi)$。……2分
第二步:根据所给函数值求$\varphi$的值
$\because f(\frac{\pi}{6})=\frac{\sqrt{3}}{2}$,$\therefore\cos(\frac{\pi}{3}+\varphi)=\frac{\sqrt{3}}{2}$,
$\therefore\frac{\pi}{3}+\varphi=\pm\frac{\pi}{6}+2k\pi$,$k\in\mathbf{Z}$,$\therefore\varphi=-\frac{\pi}{6}+2k\pi$或$\varphi=-\frac{\pi}{2}+2k\pi$,$k\in\mathbf{Z}$。$\because|\varphi|<\frac{\pi}{2}$,$\therefore\varphi=-\frac{\pi}{6}$。……4分
第三步:写出函数解析式
$\therefore f(x)=\cos(2x-\frac{\pi}{6})$。……6分
(2)第一步:求函数$g(x)$的解析式并利用两角和的正弦公式化简
$g(x)=f(x+\frac{\pi}{12})+\sqrt{3}f(x-\frac{\pi}{6})=\cos[2(x+\frac{\pi}{12})-\frac{\pi}{6}]+\sqrt{3}\cos[2(x-\frac{\pi}{6})-\frac{\pi}{6}]=\cos2x+\sqrt{3}\cos[2x-\frac{\pi}{2}-\frac{\pi}{6}]=2(\frac{1}{2}\cos2x+\frac{\sqrt{3}}{2}\sin2x)=2\sin(2x+\frac{\pi}{6})$(题眼)。……9分
第二步:令$\theta = 2x+\frac{\pi}{6}$,根据给定区间判断函数$y = 2\sin\theta$的单调性
令$\theta = 2x+\frac{\pi}{6}$,由$x\in[-\frac{\pi}{4},\frac{\pi}{4}]$,得$\theta\in[-\frac{\pi}{3},\frac{2\pi}{3}]$。
$\therefore y = 2\sin\theta$在$[-\frac{\pi}{3},\frac{\pi}{2}]$上单调递增,在$[\frac{\pi}{2},\frac{2\pi}{3}]$上单调递减。……10分
第三步:求函数$g(x)$的最值
$\therefore$当$2x+\frac{\pi}{6}=\frac{\pi}{2}$,即$x=\frac{\pi}{6}$时,$\sin(2x+\frac{\pi}{6})=1$,$g(x)$取得最大值,最大值为2。
当$2x+\frac{\pi}{6}=-\frac{\pi}{3}$,即$x=-\frac{\pi}{4}$时,$\sin(2x+\frac{\pi}{6})=-\frac{\sqrt{3}}{2}$,$g(-\frac{\pi}{4})=2×(-\frac{\sqrt{3}}{2})=-\sqrt{3}$,
当$2x+\frac{\pi}{6}=\frac{2\pi}{3}$,即$x=\frac{\pi}{4}$时,$\sin(2x+\frac{\pi}{6})=\frac{\sqrt{3}}{2}$,$g(\frac{\pi}{4})=2×\frac{\sqrt{3}}{2}=\sqrt{3}$(提示:在求函数在闭区间上的最值时,注意端点值的比较)。……11分
$\therefore g(x)$在区间$[-\frac{\pi}{4},\frac{\pi}{4}]$上的最大值为2,最小值为$-\sqrt{3}$。……13分
一两角题差多的解余弦(公2)式第化一简步:求函数$g(x)$的解析式并利用
$\because g(x)=f(x+\frac{\pi}{12})+\sqrt{3}f(x-\frac{\pi}{6})=\cos[2(x+\frac{\pi}{12})-\frac{\pi}{6}]+\sqrt{3}\cos[2(x-\frac{\pi}{6})-\frac{\pi}{6}]=2(\frac{1}{2}\cos2x+\frac{\sqrt{3}}{2}\sin2x)=2\cos(2x-\frac{\pi}{3})$。……9分
第二步;令$t = 2x-\frac{\pi}{3}$,根据给定区间判断函数$y = 2\cos t$的单调性
令$t = 2x-\frac{\pi}{3}$,由$x\in[-\frac{\pi}{4},\frac{\pi}{4}]$,得$t\in[-\frac{5\pi}{6},\frac{\pi}{6}]$。
$\therefore y = 2\cos t$在$[-\frac{5\pi}{6},0]$上单调递增,在$[0,\frac{\pi}{6}]$上单调递减。……10分
第三步:求函数$g(x)$的最值
又$2\cos(-\frac{5\pi}{6})=-\sqrt{3}$,$2\cos0 = 2$,$2\cos\frac{\pi}{6}=\sqrt{3}$。……11分
$\therefore g(x)$在区间$[-\frac{\pi}{4},\frac{\pi}{4}]$上的最大值为2,最小值为$-\sqrt{3}$。……13分
查看更多完整答案,请扫码查看


