《2026年理想树试题攻略高中数学》

16. （15分）
某罐中装有除颜色外完全相同的4个红球和3个绿球，每次随机摸出1个球.
（1）若每次都是不放回地摸球，连续摸两次，求在第二次摸球时摸得红球的条件下，第一次摸球时摸得红球的概率；
（2）若每次都是有放回地摸球，连续摸四次，摸得红球记1分，摸得绿球记0分，设四次摸球总得分为$X$，求$X$的分布列与数学期望.

答案： 16. 基础考点：条件概率、离散型随机变量的分布列与数学期望
[解]
(1)第一步：求第二次摸球时摸得红球的概率
记$R_{1}=$“第一次摸球时摸得红球”，$R_{2}=$“第二次摸球时摸得红球”，$G =$“第一次摸球时摸得绿球”，所以$P(R_{2})=P(R_{1}R_{2})+P(GR_{2})=\frac{4}{7}×\frac{3}{6}+\frac{3}{7}×\frac{4}{6}=\frac{4}{7}$(易错:注意不放回与有放回的区别，不放回时每次抽取概率在发生变化)。 4分
第二步：由条件概率公式求结果
所以$P(R_{1}|R_{2})=\frac{P(R_{1}R_{2})}{P(R_{2})}=\frac{\frac{4}{7}×\frac{3}{6}}{\frac{4}{7}}=\frac{3}{6}$。 7分
(2)第一步：确定$X$的所有可能取值
依题意，$X\sim B(4,\frac{4}{7})$(关键:有放回时，摸球得分服从二项分布)，$X$的所有可能取值为$0$、$1$、$2$、$3$、$4$。 8分
第二步：求$X$对应取值的概率
$P(X = 0)=(\frac{3}{7})^{4}=\frac{81}{2401}$；
$P(X = 1)=C_{4}^{1}×\frac{4}{7}×(\frac{3}{7})^{3}=\frac{432}{2401}$；
$P(X = 2)=C_{4}^{2}×(\frac{4}{7})^{2}×(\frac{3}{7})^{2}=\frac{864}{2401}$；
$P(X = 3)=C_{4}^{3}×(\frac{4}{7})^{3}×\frac{3}{7}=\frac{768}{2401}$；
$P(X = 4)=(\frac{4}{7})^{4}=\frac{256}{2401}$。 13分
第三步：求$X$的分布列与数学期望
所以$X$的分布列为
|$X$|$0$|$1$|$2$|$3$|$4$|
|----|----|----|----|----|----|
|$P$|$\frac{81}{2401}$|$\frac{432}{2401}$|$\frac{864}{2401}$|$\frac{768}{2401}$|$\frac{256}{2401}$|
所以$E(X)=4×\frac{4}{7}=\frac{16}{7}$。 15分

17. （15分）
如图，在四棱锥$P - A B C D$中，$P A \perp$平面$A B C D$，$B C \perp A C$，$A B // D C$.
（1）证明：平面$P B C \perp$平面$P A C$.
（2）若$B C = 2$，$C D = 3$，$P A = A B = 4$，$A D = \sqrt { 3 }$，$P$，$A$，$B$，$C$在同一个球面上，球心为$O$.
（ⅰ）求$DO$与平面$P B C$所成角的正弦值；
（ⅱ）设$\overrightarrow { P H } = \lambda \overrightarrow { P D }$，$N$为$P C$的中点且$H$，$A$，$O$，$N$四点共面，求实数$\lambda$的值.

答案：
17. 经典题型：线面垂直的判定定理与性质、面面垂直的判定定理、线面角
(1)[证明]第一步：由线面垂直的性质证$PA\perp BC$
因为$PA\perp$平面$ABCD$，$BC\subset$平面$ABCD$，所以$PA\perp BC$。 1分
第二步：利用线面垂直的判定定理证$BC\perp$平面$PAC$
又$BC\perp AC$，$AC\subset$平面$PAC$，$AC\cap PA = A$，所以$BC\perp$平面$PAC$。 3分
第三步：利用面面垂直的判定定理证结论
又$BC\subset$平面$PBC$，所以平面$PBC\perp$平面$PAC$。 4分
(2)[解](i)第一步：建立空间直角坐标系，求出相关点的坐标与相关向量的坐标
在四边形$ABCD$中，因为$AB// DC$，$BC\perp AC$，$BC = 2$，$CD = 3$，$AB = 4$，$AD=\sqrt{3}$，所以$AD\perp AB$。以$A$为坐标原点，$AB$、$AD$、$AP$所在直线分别为$x$轴、$y$轴、$z$轴建立如图所示的空间直角坐标系。

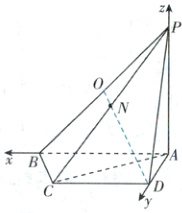
因为$BC\perp$平面$PAC$，$PC\subset$平面$PAC$，所以$BC\perp PC$，所以$\triangle PBC$与$\triangle PBA$均为直角三角形，又$P$、$A$、$B$、$C$在同一球面上，球心为$O$，所以$O$为$PB$的中点(提示:若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心)。易知$B(4,0,0)$，$C(3,\sqrt{3},0)$，$P(0,0,4)$，$D(0,\sqrt{3},0)$，$O(2,0,2)$，所以$\overrightarrow{DO}=(2,-\sqrt{3},2)$，$\overrightarrow{PB}=(4,0,-4)$，$\overrightarrow{BC}=(-1,\sqrt{3},0)$。 7分
第二步：求平面$PBC$的法向量
设平面$PBC$的法向量为$\vec{n}=(x,y,z)$，则$\begin{cases}\overrightarrow{PB}·\vec{n}=0\\\overrightarrow{BC}·\vec{n}=0\end{cases}$，即$\begin{cases}4x - 4z = 0\\-x+\sqrt{3}y = 0\end{cases}$，令$x = 1$，得$y=\frac{\sqrt{3}}{3}$，$z = 1$，所以$\vec{n}=(1,\frac{\sqrt{3}}{3},1)$。 8分
第三步：由空间夹角公式求结果
设$\overrightarrow{DO}$与平面$PBC$所成的角为$\theta$，则$\sin\theta=|\cos\langle\vec{n},\overrightarrow{DO}\rangle|=\frac{|\vec{n}·\overrightarrow{DO}|}{|\vec{n}|·|\overrightarrow{DO}|}=\frac{|2×1+(-\sqrt{3})×\frac{\sqrt{3}}{3}+2×1|}{\sqrt{1^{2}+(\frac{\sqrt{3}}{3})^{2}+1^{2}}·\sqrt{2^{2}+(-\sqrt{3})^{2}+2^{2}}}=\frac{3}{\sqrt{7}×\sqrt{11}}=\frac{3\sqrt{231}}{77}$。 10分
(ii)第一步：求向量$\overrightarrow{AO}$、$\overrightarrow{AN}$
因为$N$为$PC$的中点，所以$N(\frac{3}{2},\frac{\sqrt{3}}{2},2)$，又$A(0,0,0)$，所以$\overrightarrow{AO}=(2,0,2)$，$\overrightarrow{AN}=(\frac{3}{2},\frac{\sqrt{3}}{2},2)$。
第二步：求向量$\overrightarrow{AH}$
由(i)知$\overrightarrow{PD}=(0,\sqrt{3},-4)$，$\overrightarrow{AP}=(0,0,4)$，所以$\overrightarrow{AH}=\overrightarrow{AP}+\lambda\overrightarrow{PD}=(0,0,4)+\lambda(0,\sqrt{3},-4)=(0,\sqrt{3}\lambda,4(1 - \lambda))$。
第三步：根据四点共面建立等量关系求$\lambda$的值
因为$H$、$A$、$O$、$N$四点共面，所以存在实数$a$、$b$使得$\overrightarrow{AH}=a\overrightarrow{AO}+b\overrightarrow{AN}$(关键:根据四点共面建立向量间的关系)，即$(0,\sqrt{3}\lambda,4(1 - \lambda))=a(2,0,2)+b(\frac{3}{2},\frac{\sqrt{3}}{2},2)=(2a+\frac{3}{2}b,\frac{\sqrt{3}}{2}b,2a + 2b)$，所以$\begin{cases}0 = 2a+\frac{3}{2}b\\\sqrt{3}\lambda=\frac{\sqrt{3}}{2}b\\4(1 - \lambda)=2a + 2b\end{cases}$，解得$\lambda=\frac{4}{5}$。 15分