2026年理想树试题攻略高中数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年理想树试题攻略高中数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 正方体$A B C D - A _ { 1 } B _ { 1 } C _ { 1 } D _ { 1 }$中,$A B = 2$,$E$是棱$A B$上的动点(含端点),则(
A.$A _ { 1 } E + E C$的最小值为$2 \sqrt { 6 }$
B.若$E$是棱$A B$的中点,则点$A _ { 1 }$到平面$E B _ { 1 } D$的距离为$\frac { 2 \sqrt { 6 } } { 3 }$
C.记四棱锥$A _ { 1 } - A B C D$外接球的球心为$O$,则直线$O E$与平面$A B C D$所成角的正切值的取值范围为$\left[ \frac { \sqrt { 2 } } { 2 }, 1 \right]$
D.若$M$,$N$分别是棱$B C$,$C C _ { 1 }$的中点,则$\overrightarrow { N E }$在$\overrightarrow { N M }$上的投影向量的模为定值
BCD
)A.$A _ { 1 } E + E C$的最小值为$2 \sqrt { 6 }$
B.若$E$是棱$A B$的中点,则点$A _ { 1 }$到平面$E B _ { 1 } D$的距离为$\frac { 2 \sqrt { 6 } } { 3 }$
C.记四棱锥$A _ { 1 } - A B C D$外接球的球心为$O$,则直线$O E$与平面$A B C D$所成角的正切值的取值范围为$\left[ \frac { \sqrt { 2 } } { 2 }, 1 \right]$
D.若$M$,$N$分别是棱$B C$,$C C _ { 1 }$的中点,则$\overrightarrow { N E }$在$\overrightarrow { N M }$上的投影向量的模为定值
答案:
10.BCD 热门考点空间两线段和的最小值问题、点到平面的距离的求解、线面角、空间向量的投影向量
[深度解析]对于A,将平面$AA_1B_1B$沿$AB$翻折至与平面$ABCD$共面,连接$A_1C$,如图①,则$A_1E + EC\geq A_1C = \sqrt{4^2 + 2^2}=2\sqrt{5}$,故A错误。
对于B,若$E$是棱$AB$的中点,则$DE = B_1E$,即$\triangle DB_1E$是等腰三角形,设$DB_1$的中点为$O$,则$DE = B_1E = \sqrt{5}$,$DB_1 = 2\sqrt{3}$,所以$EO = \sqrt{DE^2 - (\frac{1}{2}DB_1)^2}=\sqrt{2}$,所以$S_{\triangle DEB_1}=\frac{1}{2}· DB_1· EO=\frac{1}{2}×2\sqrt{3}×\sqrt{2}=\sqrt{6}$,$S_{\triangle A_1EB_1}=\frac{1}{2}×2×2 = 2$。设点$A_1$到平面$EB_1D$的距离为$d$,因为$V_{A_1 - EB_1D}=V_{D - A_1EB_1}$,即$\frac{1}{3}S_{\triangle DEB_1}· d=\frac{1}{3}S_{\triangle A_1EB_1}· DA$,所以$d = \frac{S_{\triangle A_1EB_1}· DA}{S_{\triangle DEB_1}}=\frac{2×2}{\sqrt{6}}=\frac{2\sqrt{6}}{3}$,故B正确。

对于C,四棱锥$A_1 - ABCD$外接球的球心即为该正方体的外接球球心,即为点$O$,设点$O$在平面$ABCD$的投影为点$O_1$,边$AB$的中点为$F$,连接$O_1F$,$O_1E$,$OF$,$OE$(图略),则直线$OE$与平面$ABCD$所成角为$\angle OEO_1$,$\tan\angle OEO_1 = \frac{OO_1}{O_1E}$,$1\leq O_1E\leq\sqrt{2}$。当点$E$与点$F$重合时,直线$OE$与平面$ABCD$所成角最大,此时$OO_1 = 1$,$O_1E = 1$,其所成角的正切值为$\frac{OO_1}{O_1E}=1$;当点$E$与点$A$或点$B$重合时,直线$OE$与平面$ABCD$所成角最小,此时$OO_1 = 1$,$O_1E = \sqrt{2}$,其所成角的正切值为$\frac{OO_1}{O_1E}=\frac{\sqrt{2}}{2}$,所以直线$OE$与平面$ABCD$所成角的正切值的取值范围为$[\frac{\sqrt{2}}{2},1]$,故C正确。
对于D,延长$NM$交$B_1B$的延长线于点$P$,因为$M$,$N$分别是棱$BC$,$CC_1$的中点,所以$BP = NC$。过点$B$作$BQ\perp NP$,垂足为$Q$,连接$AQ$,$EQ$,如图②。
(下面证明$MN\perp$平面$ABQ$,从而得到$MN\perp EQ$)因为$AB\perp$平面$BCC_1B_1$,$MN\subset$平面$BCC_1B_1$,所以$AB\perp MN$,又$MN\perp BQ$,且$AB\cap BQ = B$,$AB$,$BQ\subset$平面$ABQ$,所以$MN\perp$平面$ABQ$。因为$EQ\subset$平面$ABQ$,所以$MN\perp EQ$,即当$E$是棱$AB$上的动点时,$\overrightarrow{NQ}$即为$\overrightarrow{NE}$在$\overrightarrow{NM}$上的投影向量,因为$|\overrightarrow{NQ}|$为定值,故D正确。故选BCD。

一题多解 对于A,证明同上。连接$A_1D$,以$D$为坐标原点,$DA$所在直线为$x$轴,$DC$所在直线为$y$轴,$DD_1$所在直线为$z$轴,建立如图所示的空间直角坐标系,设$AE = x$,则$E(2,x,0)$,$A_1(2,0,2)$,$B_1(2,2,2)$,$D(0,0,0)$。
对于B,若$E$是棱$AB$的中点,则$E(2,1,0)$,$\overrightarrow{DA_1}=(2,0,2)$,$\overrightarrow{DE}=(2,1,0)$,$\overrightarrow{EB_1}=(0,1,2)$。设平面$EB_1D$的法向量为$n = (a,y,z)$,则$\begin{cases}n·\overrightarrow{DE}=0\\n·\overrightarrow{EB_1}=0\end{cases}$,即$\begin{cases}2a + y = 0\\y + 2z = 0\end{cases}$,令$a = 1$,则平面$EB_1D$的一个法向量$n = (1,-2,1)$,所以点$A_1$到平面$EB_1D$的距离$d = \frac{|\overrightarrow{DA_1}· n|}{|n|}=\frac{4}{\sqrt{6}}=\frac{2\sqrt{6}}{3}$,故B正确。
对于C,四棱锥$A_1 - ABCD$外接球的心即为该正方体的外接球球心,所以$O(1,1,1)$,则$\overrightarrow{OE}=(1,x - 1,-1)$。平面$ABCD$的一个法向量为$m = (0,0,1)$,设直线$OE$与平面$ABCD$所成角为$\theta$,$\theta\in(0,\frac{\pi}{2})$,则$\sin\theta = |\cos\langle m,\overrightarrow{OE}\rangle| = \frac{|m·\overrightarrow{OE}|}{|m||\overrightarrow{OE}|}=\frac{1}{\sqrt{(x - 1)^2 + 2}}$,所以$\cos\theta = \frac{\sqrt{(x - 1)^2 + 1}}{\sqrt{(x - 1)^2 + 2}}$,则$\tan\theta = \frac{1}{\sqrt{(x - 1)^2 + 1}}$,因为$0\leq x\leq2$,所以$(x - 1)^2 + 1\in[1,2]$,$\frac{1}{\sqrt{(x - 1)^2 + 1}}\in[\frac{\sqrt{2}}{2},1]$,所以直线$OE$与平面$ABCD$所成角的正切值的取值范围为$[\frac{\sqrt{2}}{2},1]$,故C正确。
对于D,$N(0,2,1)$,$M(1,2,0)$,记向量$\overrightarrow{NE}$与$\overrightarrow{NM}$的夹角为$\beta$,则$\overrightarrow{NE}$在$\overrightarrow{NM}$上的投影向量的模为$|\overrightarrow{NE}\cos\beta| = |\overrightarrow{NE}·\frac{\overrightarrow{NM}}{|\overrightarrow{NM}|}| = \frac{|\overrightarrow{NE}·\overrightarrow{NM}|}{|\overrightarrow{NM}|}$,又$\overrightarrow{NE}=(2,x - 2,-1)$,$\overrightarrow{NM}=(1,0,-1)$,则$\frac{|\overrightarrow{NE}·\overrightarrow{NM}|}{|\overrightarrow{NM}|}=\frac{|2×1 + 0 + (-1)×(-1)|}{\sqrt{1^2 + 0^2 + (-1)^2}}=\frac{3}{\sqrt{2}}=\frac{3\sqrt{2}}{2}$为定值,故D正确。故选BCD。
10.BCD 热门考点空间两线段和的最小值问题、点到平面的距离的求解、线面角、空间向量的投影向量
[深度解析]对于A,将平面$AA_1B_1B$沿$AB$翻折至与平面$ABCD$共面,连接$A_1C$,如图①,则$A_1E + EC\geq A_1C = \sqrt{4^2 + 2^2}=2\sqrt{5}$,故A错误。
对于B,若$E$是棱$AB$的中点,则$DE = B_1E$,即$\triangle DB_1E$是等腰三角形,设$DB_1$的中点为$O$,则$DE = B_1E = \sqrt{5}$,$DB_1 = 2\sqrt{3}$,所以$EO = \sqrt{DE^2 - (\frac{1}{2}DB_1)^2}=\sqrt{2}$,所以$S_{\triangle DEB_1}=\frac{1}{2}· DB_1· EO=\frac{1}{2}×2\sqrt{3}×\sqrt{2}=\sqrt{6}$,$S_{\triangle A_1EB_1}=\frac{1}{2}×2×2 = 2$。设点$A_1$到平面$EB_1D$的距离为$d$,因为$V_{A_1 - EB_1D}=V_{D - A_1EB_1}$,即$\frac{1}{3}S_{\triangle DEB_1}· d=\frac{1}{3}S_{\triangle A_1EB_1}· DA$,所以$d = \frac{S_{\triangle A_1EB_1}· DA}{S_{\triangle DEB_1}}=\frac{2×2}{\sqrt{6}}=\frac{2\sqrt{6}}{3}$,故B正确。

对于C,四棱锥$A_1 - ABCD$外接球的球心即为该正方体的外接球球心,即为点$O$,设点$O$在平面$ABCD$的投影为点$O_1$,边$AB$的中点为$F$,连接$O_1F$,$O_1E$,$OF$,$OE$(图略),则直线$OE$与平面$ABCD$所成角为$\angle OEO_1$,$\tan\angle OEO_1 = \frac{OO_1}{O_1E}$,$1\leq O_1E\leq\sqrt{2}$。当点$E$与点$F$重合时,直线$OE$与平面$ABCD$所成角最大,此时$OO_1 = 1$,$O_1E = 1$,其所成角的正切值为$\frac{OO_1}{O_1E}=1$;当点$E$与点$A$或点$B$重合时,直线$OE$与平面$ABCD$所成角最小,此时$OO_1 = 1$,$O_1E = \sqrt{2}$,其所成角的正切值为$\frac{OO_1}{O_1E}=\frac{\sqrt{2}}{2}$,所以直线$OE$与平面$ABCD$所成角的正切值的取值范围为$[\frac{\sqrt{2}}{2},1]$,故C正确。
对于D,延长$NM$交$B_1B$的延长线于点$P$,因为$M$,$N$分别是棱$BC$,$CC_1$的中点,所以$BP = NC$。过点$B$作$BQ\perp NP$,垂足为$Q$,连接$AQ$,$EQ$,如图②。
(下面证明$MN\perp$平面$ABQ$,从而得到$MN\perp EQ$)因为$AB\perp$平面$BCC_1B_1$,$MN\subset$平面$BCC_1B_1$,所以$AB\perp MN$,又$MN\perp BQ$,且$AB\cap BQ = B$,$AB$,$BQ\subset$平面$ABQ$,所以$MN\perp$平面$ABQ$。因为$EQ\subset$平面$ABQ$,所以$MN\perp EQ$,即当$E$是棱$AB$上的动点时,$\overrightarrow{NQ}$即为$\overrightarrow{NE}$在$\overrightarrow{NM}$上的投影向量,因为$|\overrightarrow{NQ}|$为定值,故D正确。故选BCD。

一题多解 对于A,证明同上。连接$A_1D$,以$D$为坐标原点,$DA$所在直线为$x$轴,$DC$所在直线为$y$轴,$DD_1$所在直线为$z$轴,建立如图所示的空间直角坐标系,设$AE = x$,则$E(2,x,0)$,$A_1(2,0,2)$,$B_1(2,2,2)$,$D(0,0,0)$。
对于B,若$E$是棱$AB$的中点,则$E(2,1,0)$,$\overrightarrow{DA_1}=(2,0,2)$,$\overrightarrow{DE}=(2,1,0)$,$\overrightarrow{EB_1}=(0,1,2)$。设平面$EB_1D$的法向量为$n = (a,y,z)$,则$\begin{cases}n·\overrightarrow{DE}=0\\n·\overrightarrow{EB_1}=0\end{cases}$,即$\begin{cases}2a + y = 0\\y + 2z = 0\end{cases}$,令$a = 1$,则平面$EB_1D$的一个法向量$n = (1,-2,1)$,所以点$A_1$到平面$EB_1D$的距离$d = \frac{|\overrightarrow{DA_1}· n|}{|n|}=\frac{4}{\sqrt{6}}=\frac{2\sqrt{6}}{3}$,故B正确。
对于C,四棱锥$A_1 - ABCD$外接球的心即为该正方体的外接球球心,所以$O(1,1,1)$,则$\overrightarrow{OE}=(1,x - 1,-1)$。平面$ABCD$的一个法向量为$m = (0,0,1)$,设直线$OE$与平面$ABCD$所成角为$\theta$,$\theta\in(0,\frac{\pi}{2})$,则$\sin\theta = |\cos\langle m,\overrightarrow{OE}\rangle| = \frac{|m·\overrightarrow{OE}|}{|m||\overrightarrow{OE}|}=\frac{1}{\sqrt{(x - 1)^2 + 2}}$,所以$\cos\theta = \frac{\sqrt{(x - 1)^2 + 1}}{\sqrt{(x - 1)^2 + 2}}$,则$\tan\theta = \frac{1}{\sqrt{(x - 1)^2 + 1}}$,因为$0\leq x\leq2$,所以$(x - 1)^2 + 1\in[1,2]$,$\frac{1}{\sqrt{(x - 1)^2 + 1}}\in[\frac{\sqrt{2}}{2},1]$,所以直线$OE$与平面$ABCD$所成角的正切值的取值范围为$[\frac{\sqrt{2}}{2},1]$,故C正确。
对于D,$N(0,2,1)$,$M(1,2,0)$,记向量$\overrightarrow{NE}$与$\overrightarrow{NM}$的夹角为$\beta$,则$\overrightarrow{NE}$在$\overrightarrow{NM}$上的投影向量的模为$|\overrightarrow{NE}\cos\beta| = |\overrightarrow{NE}·\frac{\overrightarrow{NM}}{|\overrightarrow{NM}|}| = \frac{|\overrightarrow{NE}·\overrightarrow{NM}|}{|\overrightarrow{NM}|}$,又$\overrightarrow{NE}=(2,x - 2,-1)$,$\overrightarrow{NM}=(1,0,-1)$,则$\frac{|\overrightarrow{NE}·\overrightarrow{NM}|}{|\overrightarrow{NM}|}=\frac{|2×1 + 0 + (-1)×(-1)|}{\sqrt{1^2 + 0^2 + (-1)^2}}=\frac{3}{\sqrt{2}}=\frac{3\sqrt{2}}{2}$为定值,故D正确。故选BCD。
11. 已知函数$f ( x ) = \left\{ \begin{array} { l } { \mathrm { e } ^ { x }, x \leq 0, } \\ { \ln x + 1, x > 0, } \end{array} \right.$方程$f ( f ( x ) ) = m$有三个不同的实根$x _ { 1 }$,$x _ { 2 }$,$x _ { 3 }$,则( )
A.方程$f ( x ) = m$有两个不同的实根
B.$m \in [ 1, \mathrm { e } ]$
C.$m - 1$是方程$f ( f ( x ) ) = m$的一个根
D.$x _ { 1 } + x _ { 2 } + x _ { 3 } < \mathrm { e } + \frac { 1 } { \mathrm { e } }$
A.方程$f ( x ) = m$有两个不同的实根
B.$m \in [ 1, \mathrm { e } ]$
C.$m - 1$是方程$f ( f ( x ) ) = m$的一个根
D.$x _ { 1 } + x _ { 2 } + x _ { 3 } < \mathrm { e } + \frac { 1 } { \mathrm { e } }$
答案:
11.ACD 经典题型根据方程根的个数求参数的范围、函数与方程的综合应用
思路导引:令$t = f(x)$,考虑$f(t) = m$的解,画出$f(t)$的图象。
对于A:由题意$\rightarrow f(t) = m$有两个不同解$t_1$,$t_2$且$t_1\leq0$,$\frac{1}{e}<t_2\leq1\rightarrow A$正确;
对于B:由A可知$0<m\leq1\rightarrow B$错误;
对于C:$0<m\leq1\rightarrow m - 1\leq0\rightarrow f(m - 1)=e^{m - 1}$,$f(e^{m - 1})=m\rightarrow f(f(m - 1))=m\rightarrow C$正确;
对于D:设$f(x)=t_2$有两个不同解为$x_1$,$x_2$,且$x_1<x_2$,则$x_1=\ln t_2$,$x_2=e^{t_2}-1$,$f(x)=t_1$有唯一解为$x_3$,则$x_3=e^{t_1 - 1}$,用$t_1$,$t_2$表示$x_1 + x_2 + x_3$,$\frac{t_1=\ln m}{t_2=e^{m - 1}}$用$m$表示$x_1 + x_2 + x_3$,构造函数$g(m)$,研究$g(m)$的单调性$\rightarrow g(m)$的范围$\rightarrow D$正确
[深度解析]令$t = f(x)$,考虑$f(t) = m$的解(关键:通过“换元解套”将原方程拆解为两个方程)。$f(t)$的图象如图,
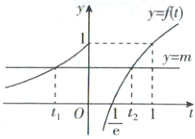
对于A,因为$f(f(x)) = m$有三个不同的解,故$f(t) = m$有两个不同的解$t_1$,$t_2$,且$t_1\leq0$,$\frac{1}{e}<t_2\leq1$,所以方程$f(x)=m$有两个不同的实根。故A正确。
对于B,由A的分析可得$0<m\leq1$,故B错误。
对于C,由B知,$0<m\leq1$,所以$m - 1\leq0$,所以$f(m - 1)=e^{m - 1}$,而$0<e^{m - 1}\leq1$,所以$f(e^{m - 1})=\ln e^{m - 1}+1=m - 1 + 1=m$,所以$f(f(m - 1))=f(e^{m - 1})=m$,故C正确。
对于D,由A的分析可得$f(x)=t_2$有两个不同的解,不妨设为$x_1$,$x_2$,且$x_1<x_2$,$f(x)=t_1$有唯一解,不妨设为$x_3$,则$e^{t_2}=\ln x_2 + 1 = t_2$,$\ln x_1 + 1 = t_1$,故$x_1=\ln t_2$,$x_2=e^{t_2}-1$,$x_3=e^{t_1 - 1}$(关键:利用$t_1$,$t_2$表示$x_1$,$x_2$
11.ACD 经典题型根据方程根的个数求参数的范围、函数与方程的综合应用
思路导引:令$t = f(x)$,考虑$f(t) = m$的解,画出$f(t)$的图象。
对于A:由题意$\rightarrow f(t) = m$有两个不同解$t_1$,$t_2$且$t_1\leq0$,$\frac{1}{e}<t_2\leq1\rightarrow A$正确;
对于B:由A可知$0<m\leq1\rightarrow B$错误;
对于C:$0<m\leq1\rightarrow m - 1\leq0\rightarrow f(m - 1)=e^{m - 1}$,$f(e^{m - 1})=m\rightarrow f(f(m - 1))=m\rightarrow C$正确;
对于D:设$f(x)=t_2$有两个不同解为$x_1$,$x_2$,且$x_1<x_2$,则$x_1=\ln t_2$,$x_2=e^{t_2}-1$,$f(x)=t_1$有唯一解为$x_3$,则$x_3=e^{t_1 - 1}$,用$t_1$,$t_2$表示$x_1 + x_2 + x_3$,$\frac{t_1=\ln m}{t_2=e^{m - 1}}$用$m$表示$x_1 + x_2 + x_3$,构造函数$g(m)$,研究$g(m)$的单调性$\rightarrow g(m)$的范围$\rightarrow D$正确
[深度解析]令$t = f(x)$,考虑$f(t) = m$的解(关键:通过“换元解套”将原方程拆解为两个方程)。$f(t)$的图象如图,

对于A,因为$f(f(x)) = m$有三个不同的解,故$f(t) = m$有两个不同的解$t_1$,$t_2$,且$t_1\leq0$,$\frac{1}{e}<t_2\leq1$,所以方程$f(x)=m$有两个不同的实根。故A正确。
对于B,由A的分析可得$0<m\leq1$,故B错误。
对于C,由B知,$0<m\leq1$,所以$m - 1\leq0$,所以$f(m - 1)=e^{m - 1}$,而$0<e^{m - 1}\leq1$,所以$f(e^{m - 1})=\ln e^{m - 1}+1=m - 1 + 1=m$,所以$f(f(m - 1))=f(e^{m - 1})=m$,故C正确。
对于D,由A的分析可得$f(x)=t_2$有两个不同的解,不妨设为$x_1$,$x_2$,且$x_1<x_2$,$f(x)=t_1$有唯一解,不妨设为$x_3$,则$e^{t_2}=\ln x_2 + 1 = t_2$,$\ln x_1 + 1 = t_1$,故$x_1=\ln t_2$,$x_2=e^{t_2}-1$,$x_3=e^{t_1 - 1}$(关键:利用$t_1$,$t_2$表示$x_1$,$x_2$
12. 等差数列$\{ a _ { n } \}$的公差为$2$,记其前$n$项和为$S _ { n }$,若$S _ { 11 } = 11$,则$a _ { 1 } =$
-9
。
答案:
12. -9
13. 平面直角坐标系中,直线$y = a$与$y$轴,曲线$y = 2 \ln x$的交点分别为$A$,$B$,若曲线$y = 2 \ln x$在$B$点处的切线交$y$轴于$C$点,则$\vert A C \vert =$
2
。
答案:
13. 2
14. 直线$l$过双曲线$C : \frac { x ^ { 2 } } { a ^ { 2 } } - \frac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a > 0, b > 0 )$的左焦点$F$,交$C$的渐近线于$A$,$B$两点。若$\overrightarrow { F B } = 3 \overrightarrow { F A }$,且$\vert \overrightarrow { F A } \vert = b$,则$C$的离心率为
$\sqrt{3}$
。
答案:
14. $\sqrt{3}$
15. (13分)
如图,在直三棱柱$A B C - A _ { 1 } B _ { 1 } C _ { 1 }$中,$A A _ { 1 } = A B = \frac { 1 } { 2 } A C = 2$,$A B \perp B C$。
(1) 求证:$A B _ { 1 } \perp$平面$A _ { 1 } B C$。
(2) 求平面$A _ { 1 } B C$与平面$A _ { 1 } A C C _ { 1 }$的夹角的余弦值。

如图,在直三棱柱$A B C - A _ { 1 } B _ { 1 } C _ { 1 }$中,$A A _ { 1 } = A B = \frac { 1 } { 2 } A C = 2$,$A B \perp B C$。
(1) 求证:$A B _ { 1 } \perp$平面$A _ { 1 } B C$。
(2) 求平面$A _ { 1 } B C$与平面$A _ { 1 } A C C _ { 1 }$的夹角的余弦值。

答案:
(1)
以$B$为原点,分别以$BC,BA,BB_1$所在直线为$x,y,z$轴建立空间直角坐标系。
已知$AA_1 = AB=\frac{1}{2}AC = 2$,$AB\perp BC$,则$A(0,2,0)$,$B_1(0,0,2)$,$A_1(0,2,2)$,$C(2\sqrt{3},0,0)$,$B(0,0,0)$。
$\overrightarrow{AB_1}=(0 - 0,0 - 2,2 - 0)=(0,-2,2)$,$\overrightarrow{A_1B}=(0 - 0,0 - 2,0 - 2)=(0,-2,-2)$,$\overrightarrow{BC}=(2\sqrt{3},0,0)$。
$\overrightarrow{AB_1}·\overrightarrow{A_1B}=0×0+(-2)×(-2)+2×(-2)=0$,$\overrightarrow{AB_1}·\overrightarrow{BC}=0×2\sqrt{3}+(-2)×0 + 2×0=0$。
所以$\overrightarrow{AB_1}\perp\overrightarrow{A_1B}$,$\overrightarrow{AB_1}\perp\overrightarrow{BC}$,即$AB_1\perp A_1B$,$AB_1\perp BC$。
因为$A_1B\cap BC = B$,所以$AB_1\perp$平面$A_1BC$。
(2)
设平面$A_1BC$的法向量为$\overrightarrow{n_1}=(x_1,y_1,z_1)$,由$\begin{cases}\overrightarrow{n_1}·\overrightarrow{A_1B}=0\\\overrightarrow{n_1}·\overrightarrow{BC}=0\end{cases}$,即$\begin{cases}-2y_1-2z_1 = 0\\2\sqrt{3}x_1=0\end{cases}$。
令$y_1 = 1$,则$z_1=-1$,$x_1 = 0$,所以$\overrightarrow{n_1}=(0,1,-1)$。
设平面$A_1ACC_1$的法向量为$\overrightarrow{n_2}=(x_2,y_2,z_2)$,$\overrightarrow{AC}=(2\sqrt{3},-2,0)$,$\overrightarrow{AA_1}=(0,0,2)$。
由$\begin{cases}\overrightarrow{n_2}·\overrightarrow{AC}=0\\\overrightarrow{n_2}·\overrightarrow{AA_1}=0\end{cases}$,即$\begin{cases}2\sqrt{3}x_2-2y_2=0\\2z_2=0\end{cases}$。
令$x_2 = 1$,则$y_2=\sqrt{3}$,$z_2 = 0$,所以$\overrightarrow{n_2}=(1,\sqrt{3},0)$。
设平面$A_1BC$与平面$A_1ACC_1$的夹角为$\theta$,$\cos\theta=\frac{\vert\overrightarrow{n_1}·\overrightarrow{n_2}\vert}{\vert\overrightarrow{n_1}\vert\vert\overrightarrow{n_2}\vert}=\frac{\vert0×1 + 1×\sqrt{3}+(-1)×0\vert}{\sqrt{0 + 1+1}×\sqrt{1 + 3+0}}=\frac{\sqrt{3}}{\sqrt{2}×2}=\frac{\sqrt{6}}{4}$。
综上,答案为:
(1) 证明过程如上述;
(2) $\frac{\sqrt{6}}{4}$。
(1)
以$B$为原点,分别以$BC,BA,BB_1$所在直线为$x,y,z$轴建立空间直角坐标系。
已知$AA_1 = AB=\frac{1}{2}AC = 2$,$AB\perp BC$,则$A(0,2,0)$,$B_1(0,0,2)$,$A_1(0,2,2)$,$C(2\sqrt{3},0,0)$,$B(0,0,0)$。
$\overrightarrow{AB_1}=(0 - 0,0 - 2,2 - 0)=(0,-2,2)$,$\overrightarrow{A_1B}=(0 - 0,0 - 2,0 - 2)=(0,-2,-2)$,$\overrightarrow{BC}=(2\sqrt{3},0,0)$。
$\overrightarrow{AB_1}·\overrightarrow{A_1B}=0×0+(-2)×(-2)+2×(-2)=0$,$\overrightarrow{AB_1}·\overrightarrow{BC}=0×2\sqrt{3}+(-2)×0 + 2×0=0$。
所以$\overrightarrow{AB_1}\perp\overrightarrow{A_1B}$,$\overrightarrow{AB_1}\perp\overrightarrow{BC}$,即$AB_1\perp A_1B$,$AB_1\perp BC$。
因为$A_1B\cap BC = B$,所以$AB_1\perp$平面$A_1BC$。
(2)
设平面$A_1BC$的法向量为$\overrightarrow{n_1}=(x_1,y_1,z_1)$,由$\begin{cases}\overrightarrow{n_1}·\overrightarrow{A_1B}=0\\\overrightarrow{n_1}·\overrightarrow{BC}=0\end{cases}$,即$\begin{cases}-2y_1-2z_1 = 0\\2\sqrt{3}x_1=0\end{cases}$。
令$y_1 = 1$,则$z_1=-1$,$x_1 = 0$,所以$\overrightarrow{n_1}=(0,1,-1)$。
设平面$A_1ACC_1$的法向量为$\overrightarrow{n_2}=(x_2,y_2,z_2)$,$\overrightarrow{AC}=(2\sqrt{3},-2,0)$,$\overrightarrow{AA_1}=(0,0,2)$。
由$\begin{cases}\overrightarrow{n_2}·\overrightarrow{AC}=0\\\overrightarrow{n_2}·\overrightarrow{AA_1}=0\end{cases}$,即$\begin{cases}2\sqrt{3}x_2-2y_2=0\\2z_2=0\end{cases}$。
令$x_2 = 1$,则$y_2=\sqrt{3}$,$z_2 = 0$,所以$\overrightarrow{n_2}=(1,\sqrt{3},0)$。
设平面$A_1BC$与平面$A_1ACC_1$的夹角为$\theta$,$\cos\theta=\frac{\vert\overrightarrow{n_1}·\overrightarrow{n_2}\vert}{\vert\overrightarrow{n_1}\vert\vert\overrightarrow{n_2}\vert}=\frac{\vert0×1 + 1×\sqrt{3}+(-1)×0\vert}{\sqrt{0 + 1+1}×\sqrt{1 + 3+0}}=\frac{\sqrt{3}}{\sqrt{2}×2}=\frac{\sqrt{6}}{4}$。
综上,答案为:
(1) 证明过程如上述;
(2) $\frac{\sqrt{6}}{4}$。
查看更多完整答案,请扫码查看


