1. 空间观念 求下面各圆的面积。
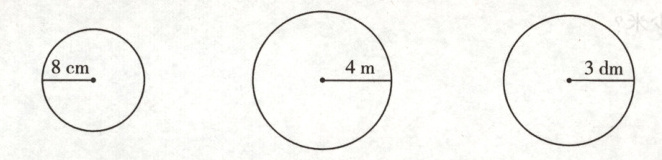

答案:
1.$3.14×8^{2}=200.96(cm^{2})$
$3.14×4^{2}=50.24(m^{2})$
$3.14×3^{2}=28.26(dm^{2})$
$3.14×4^{2}=50.24(m^{2})$
$3.14×3^{2}=28.26(dm^{2})$
2. 信息科技 在第 24 届冬奥会上,冰壶是其中的比赛项目之一。已知冰壶赛道的一端画有一个半径约为 1.8 米的圆圈作为球员的发球区,被称作本垒,本垒的占地面积约是多少平方米?(得数保留整数)
答案:
2.$3.14×1.8^{2}=10.1736(平方米)≈10$平方米
答:本垒的占地面积约是10平方米。
答:本垒的占地面积约是10平方米。
3. 易错题 一只手表的分针针尖到中心的距离是 0.8 厘米,从 12 时到 14 时,分针扫过的面积是多少平方厘米?
答案:
3.$3.14×0.8^{2}×2=4.0192$(平方厘米)
答:分针扫过的面积是4.0192平方厘米。
答:分针扫过的面积是4.0192平方厘米。
4. 应用意识 一个圆形养鱼池的半径是 10 米,如果每平方米投放 15 尾鱼苗,那么这个养鱼池一共能投放多少尾鱼苗?
答案:
4.$3.14×10^{2}×15=4710(尾)$
答:这个养鱼池一共能投放4710尾鱼苗。
答:这个养鱼池一共能投放4710尾鱼苗。
5. 开放题 用两个直角板和一个直尺测量一枚一元硬币的直径,写出操作步骤,并计算这枚一元硬币的面积。
答案:
5.将一枚一元硬币置于两个直角三角板的直角边之间,将其紧紧夹住,再将其直尺有刻度的一边紧贴两个直角三角板的直角边和硬币下方,其中一个三角板的直角边对齐直尺整刻度线位置。利用直尺得到两条直角边之间的距离,即硬币的直径。
查看更多完整答案,请扫码查看


