第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
【例】如图,如果$□ ABCD$的内角$\angle BAD$的平分线交$BC$于点$E$,且$AE = BE$。
(1)请直接写出$□ ABCD$各内角的度数;
(2)若$AB = 2$,$AD = 3$,求$□ ABCD$的面积。
【思路点拨】(1)根据平行四边形的性质及角平分线求出各角的度数;(2)平行四边形的面积等于底$×$高,底边长题干中已经告知,故要求平行四边形的面积需要求出平行四边形关于底边$BC$上的高。
【解答】

(1)请直接写出$□ ABCD$各内角的度数;
(2)若$AB = 2$,$AD = 3$,求$□ ABCD$的面积。
【思路点拨】(1)根据平行四边形的性质及角平分线求出各角的度数;(2)平行四边形的面积等于底$×$高,底边长题干中已经告知,故要求平行四边形的面积需要求出平行四边形关于底边$BC$上的高。
【解答】

答案:
(1)$\angle B = \angle D = 60^{\circ}, \angle C = \angle BAD = 120^{\circ}$.
(2)作 AH \perp BE 于点 H.由
(1)可知,$\triangle ABE$是等边三角形,$\therefore \angle BAH = 30^{\circ},BH = \frac{1}{2}BE = \frac{1}{2}AB = 1$.$\therefore$在Rt$\triangle ABH$中,$AH = \sqrt{AB^{2} - BH^{2}} = \sqrt{3}$.$\therefore S_{□ ABCD} = AD \cdot AH = 3\sqrt{3}$.
(1)$\angle B = \angle D = 60^{\circ}, \angle C = \angle BAD = 120^{\circ}$.
(2)作 AH \perp BE 于点 H.由
(1)可知,$\triangle ABE$是等边三角形,$\therefore \angle BAH = 30^{\circ},BH = \frac{1}{2}BE = \frac{1}{2}AB = 1$.$\therefore$在Rt$\triangle ABH$中,$AH = \sqrt{AB^{2} - BH^{2}} = \sqrt{3}$.$\therefore S_{□ ABCD} = AD \cdot AH = 3\sqrt{3}$.
【跟踪训练】如图,在$\triangle ABC$中,$AB = 4\mathrm{cm}$,$BC = 5\mathrm{cm}$,$\angle ABC = 30^{\circ}$,过点$A$的直线$a// BC$,$D$是直线$a$上的一个动点,则$\triangle DBC$的面积为
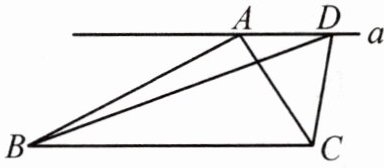
5 cm²
。
答案:
5 cm²
1. 如图,直线$a// b$,且$a$,$b$之间相距$4\mathrm{cm}$,点$P$是直线$a$上一定点,点$Q$在直线$b$上运动,则在点$Q$的运动过程中,线段$PQ$的最小值是

4 cm
。
答案:
1. 4 cm
2. (教材P126“想一想”变式)如图,直线$l_1// l_2$,$\triangle ABC$的面积为$10$,则$\triangle DBC$的面积(

A.大于$10$
B.小于$10$
C.等于$10$
D.不确定
C
)
A.大于$10$
B.小于$10$
C.等于$10$
D.不确定
答案:
2. C
3. 如图,在$□ ABCD$中,$AE\perp BC$于点$E$,$AF\perp CD$于点$F$。若$AE = 4$,$AF = 6$,$□ ABCD$的周长为$40$,则$□ ABCD$的面积为
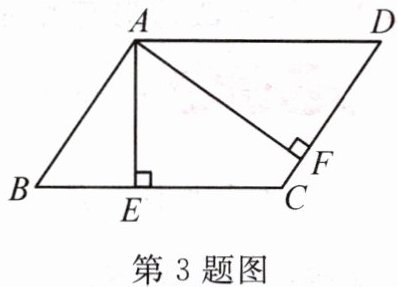
48
。
答案:
3. 48
4. 在同一平面内,设$a$,$b$,$c$是三条互相平行的直线,已知$a$与$b$的距离为$4\mathrm{cm}$,$b$与$c$的距离为$1\mathrm{cm}$,则$a$与$c$的距离为
5 cm 或 3 cm
。
答案:
4. 5 cm 或 3 cm
5. 如图,$P$是面积为$S$的$□ ABCD$内任意一点,$\triangle PAD$的面积为$S_1$,$\triangle PBC$的面积为$S_2$,则(
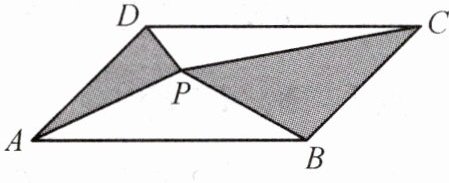
A.$S_1 + S_2>\frac{S}{2}$
B.$S_1 + S_2<\frac{S}{2}$
C.$S_1 + S_2=\frac{S}{2}$
D.$S_1 + S_2$的大小与$P$点位置有关
C
)
A.$S_1 + S_2>\frac{S}{2}$
B.$S_1 + S_2<\frac{S}{2}$
C.$S_1 + S_2=\frac{S}{2}$
D.$S_1 + S_2$的大小与$P$点位置有关
答案:
5. C
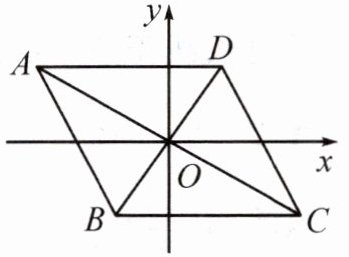
6. 如图,已知点$A(-4,2)$,$B(-1,-2)$,$□ ABCD$的对角线交于坐标原点$O$。
(1)请直接写出点$C$,$D$的坐标;
(2)写出从线段$AB$到线段$CD$的变换过程;
(3)直接写出$□ ABCD$的面积。
(1)请直接写出点$C$,$D$的坐标;
(2)写出从线段$AB$到线段$CD$的变换过程;
(3)直接写出$□ ABCD$的面积。

答案:
6. 解:
(1)C(4, -2),D(1,2).
(2)线段 AB 到线段 CD 的变换过程是:绕点 O 旋转$ 180^{\circ}.(3)S_{□ ABCD} = 20.$
(1)C(4, -2),D(1,2).
(2)线段 AB 到线段 CD 的变换过程是:绕点 O 旋转$ 180^{\circ}.(3)S_{□ ABCD} = 20.$
查看更多完整答案,请扫码查看


