第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
2. 下图中若 $ \angle 1 = 40^{\circ} $,那么 $ \angle 2 = $(
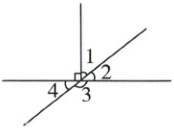
50°
),$ \angle 3 = $(130°
),$ \angle 4 = $(50°
)。(3分)
答案:
50° 130° 50°
3. 细心观察,完成下面各题。(11分)
(1)写出一组互相平行的线段:(
(2)图中有(
(3)量出 $ \angle 1 $、$ \angle 2 $、$ \angle 3 $ 的度数:$ \angle 1 = $(
(4)$ \angle 1 + \angle 2 = $(
我发现:
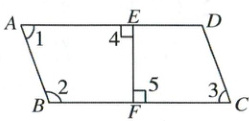
(1)写出一组互相平行的线段:(
AD//BC
);写出一组互相垂直的线段:(EF⊥BC
)。(2)图中有(
2
)个梯形。(3)量出 $ \angle 1 $、$ \angle 2 $、$ \angle 3 $ 的度数:$ \angle 1 = $(
略。
),$ \angle 2 = $(略。
),$ \angle 3 = $(略。
)。(4)$ \angle 1 + \angle 2 = $(
180°
),$ \angle 2 + \angle 3 = $(180°
)。我发现:
发现略。
。
答案:
(1)AD//BC EF⊥BC(答案不唯一)
(2)2
(3)略。
(4)180° 180° 发现略。
(1)AD//BC EF⊥BC(答案不唯一)
(2)2
(3)略。
(4)180° 180° 发现略。
1. 画出下面图形底边上的高。(6分)


答案:
1. 第一幅图(平行四边形):从平行四边形上底边相对的顶点向底边作垂线,顶点到垂足之间的线段即为底边上的高,用虚线画出,并标上垂直符号。
2. 第二幅图(梯形):从梯形上底边与所标底边相对的顶点向底边作垂线,顶点到垂足之间的线段即为底边上的高,用虚线画出,并标上垂直符号。
3. 第三幅图(平行四边形):从平行四边形上底边相对的边(非底边)上的顶点向底边作垂线,顶点到垂足之间的线段即为底边上的高,用虚线画出,并标上垂直符号。
2. 第二幅图(梯形):从梯形上底边与所标底边相对的顶点向底边作垂线,顶点到垂足之间的线段即为底边上的高,用虚线画出,并标上垂直符号。
3. 第三幅图(平行四边形):从平行四边形上底边相对的边(非底边)上的顶点向底边作垂线,顶点到垂足之间的线段即为底边上的高,用虚线画出,并标上垂直符号。
2. 以下面方格图中的两条线段为边画一个平行四边形。在平行四边形里再画一条线段,把它分成一个梯形和一个三角形。(4分)


答案:
1. 以已知两条线段的端点为顶点,利用方格纸特点,使对应边平行且相等,画出平行四边形。
假设左边线段两个端点为A、B,右边线段两个端点为C、D(与左边线段平行且长度相等),依次连接A、C、B、D形成平行四边形。
2. 在平行四边形一个顶点向对边(非相邻顶点所在的边)上的某一点(非顶点)连线,把平行四边形分成一个梯形和一个三角形。
例如从平行四边形左上角顶点向底边(非左右两个顶点)某一点连线。
假设左边线段两个端点为A、B,右边线段两个端点为C、D(与左边线段平行且长度相等),依次连接A、C、B、D形成平行四边形。
2. 在平行四边形一个顶点向对边(非相邻顶点所在的边)上的某一点(非顶点)连线,把平行四边形分成一个梯形和一个三角形。
例如从平行四边形左上角顶点向底边(非左右两个顶点)某一点连线。
1. 东东、明明和亮亮三位小朋友去同一家冷饮店买饮料。如果他们三人的行走速度相同,哪位小朋友最先买到饮料?请说明理由。(6分)
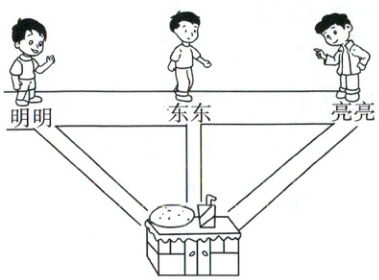

答案:
东东最先买到饮料。理由:从直线外一点到这条直线的所有线段中,垂直线段最短。
查看更多完整答案,请扫码查看


