《2025年单元测试卷山东文艺出版社四年级数学上册人教版》

1. (新题型)画一画。
在2024年巴黎奥运会上,中国运动员们取得了令人瞩目的成绩。在体育竞技的背后,数学的应用无处不在。比如：在投掷项目中,根据计算,以$45^{\circ}$角投掷一个物体,可以达到最远的距离；体操项目的转体主要是绕着人体的纵轴旋转,如$180^{\circ}$,$360^{\circ}$；乒乓球项目中抛球要求垂直向上,正常要求是$90^{\circ}$,不能偏离$30^{\circ}$以上,正手攻球前大小臂的夹角是$120^{\circ}$左右。根据上面的信息,请你选一个锐角、一个钝角和一个平角画在下面。(6分)

答案：

2. 按要求作图。(7分)
(1)画出直线$AB$；
(2)画出射线$CB$；
(3)画出线段$AC$；
(4)画好的图形中有几个角(小于平角的角)？它们分别是什么角？

答案：

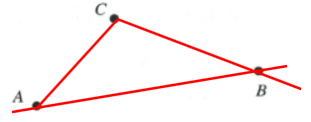
7,3个锐角，4个钝角

1. 求$∠1和∠2$的度数。(4分)

答案： ∠1=180°-90°=90° ∠2=180°-30°=150°

2. (学科融合)清代诗人高鼎有一首诗：“草长莺飞二月天,拂堤杨柳醉春烟。儿童散学归来早,忙趁东风放纸鸢。”诗中生动描绘了儿童放风筝的场景。下图画的是甲、乙两人放风筝的场景,风筝线的长度相等。(6分)
(1)量一量,甲的风筝线与地面的夹角是(70)°,乙的风筝线与地面的夹角是(45)°。
(2)风筝的高度和风筝线与地面的夹角有什么关系？(夹角在$90^{\circ}$范围内)
风筝线与地面的夹角越大,风筝的高度越高。
(3)如果丙的风筝线与地面的夹角为$35^{\circ}$(风筝线的长度与甲、乙的相等),那么他的风筝飞的高度比甲和乙的高吗？为什么？
不比甲和乙的高。丙的风筝线与地面的夹角比甲、乙的风筝线与地面的夹角都要小。

答案：
(1)70 45
(2)风筝线与地面的夹角越大,风筝的高度越高。
(3)不比甲和乙的高。丙的风筝线与地面的夹角比甲、乙的风筝线与地面的夹角都要小。