《2025年同步练习册海燕出版社三年级数学上册人教版》

1. 填一填。
(1) 像手电筒、汽车灯等射出来的光线可以看作(射线),而直尺的一条边可以看作(线段),《西游记》中孙悟空的金箍棒能向两端无限延伸,可以看作(直线)。线家族的“三兄弟”告诉我们：做事,要像(线段)那样“有始有终,坚持到底”；学习,要像(射线)那样“有始无终,勇往直前”；想象,要像(直线)那样“无始无终,自由大胆”。
(2) 两点间所有连线中(线段)最短,这条(线段)的长度叫作两点间的距离。

答案：
(1)射线 、线段 、直线 、线段、 射线 、直线；
(2)线段 、线段。

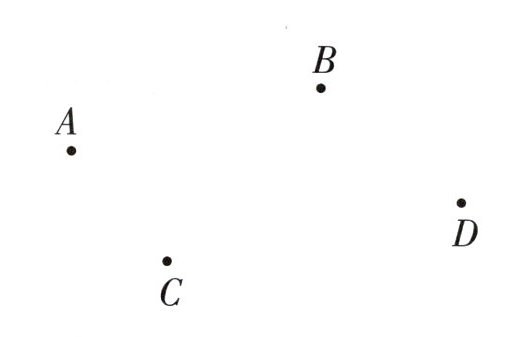
2. 按要求画图。
(1) 画出线段 $ AB $、$ AC $。
(2) 画出射线 $ AD $。
(3) 画出射线 $ BC $。

答案： （1）画线段 $AB$：用直尺连接点 $A$ 和点 $B$，形成线段 $AB$，
画线段$AC$：用直尺连接点$A$和点$C$，形成线段$AC$。
（2）画射线$AD$：从点$A$出发，经过点$D$向一方无限延伸，画出射线$AD$。
（3）画射线$BC$：从点$B$出发，经过点$C$（本题中经过$C$向$C$方向延伸，或根据射线定义也可不经过$C$向另一方向，但题目要求射线$BC$，常规理解从$B$向$C$方向）向一方无限延伸，画出射线$BC$。

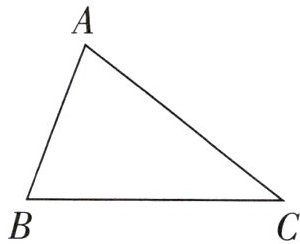
3. 明明想用下面这根铁丝围成右边的三角形,铁丝的长度够吗？请你用圆规比一比,画一画。用圆规量取线段AC长度，画到线段AB的延长线上（以B为圆心，AC长为半径画弧交BA延长线或用圆规两脚分别量AC长，在AB延长线截取），可大致判断AC + BC（通过圆规比较或同样用圆规在AC上截取BC长度等方式）的长度和小于（假设通过比较得出）铁丝长度（铁丝长度未给出具体数值，假设通过圆规比较铁丝长度与三角形三边长度之和得出），铁丝长度不够。

答案： 用圆规量取线段AC长度，画到线段AB的延长线上（以B为圆心，AC长为半径画弧交BA延长线或用圆规两脚分别量AC长，在AB延长线截取），可大致判断AC + BC（通过圆规比较或同样用圆规在AC上截取BC长度等方式）的长度和小于（假设通过比较得出）铁丝长度（铁丝长度未给出具体数值，假设通过圆规比较铁丝长度与三角形三边长度之和得出），铁丝长度不够。

4. 兔子要从点 $ A $ 出发回家,哪条路线最短？请说明理由。

答案： 答：路线①最短。
理由：两点之间所有连线中线段最短，路线①是线段，路线②和路线③是曲线（或折线），所以路线①最短。

数一数,填一填。

有(1)条直线、(10)条线段、(8)条射线。

答案： 1、10、8