《2025年同步练习册海燕出版社三年级数学上册人教版》

1. 圆规是用来(画圆)的工具,也可以用它量出同样长度的(线段)。请在右图中填出圆规各部分的名称。

手柄；规脚；铅笔脚

答案： 画圆；线段；手柄；规脚；铅笔脚

2. 明明用圆规比较线段 $ AB $ 和 $ CD $、$ EF $ 的长短。结合以下情况进行判断。

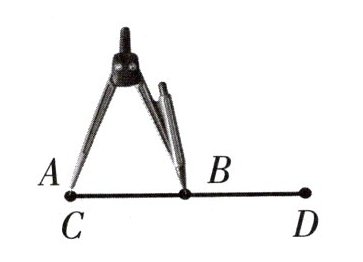
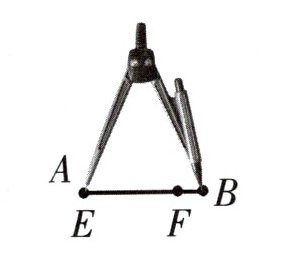
$ AB $＜$ CD $

$ AB $＞$ EF $

答案： 1. 对于$AB$与$CD$比较：
用圆规把$AB$的一端$A$与$CD$的一端$C$重合，调整圆规另一端到$B$点，保持圆规张开程度不变，将圆规另一端放到$D$点，发现$B$点在$CD$上，所以$AB\lt CD$。
2. 对于$AB$与$EF$比较：
用圆规把$AB$的一端$A$与$EF$的一端$E$重合，调整圆规另一端到$B$点，保持圆规张开程度不变，将圆规另一端放到$F$点，发现$F$点在圆规另一端与$B$点重合时圆规的范围内，即$EF$长度小于圆规张开长度（$AB$长度），所以$AB\gt EF$。
故答案依次为：$＜$；$＞$。

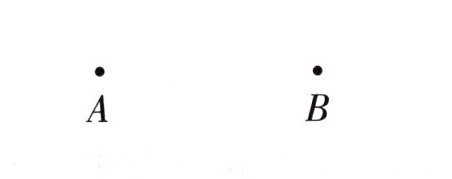
3. 过 $ A $、$ B $ 两点可以画(1)条直线 $ l $,画一画；再用圆规在直线 $ l $ 上作一条与线段 $ AB $ 同样长的线段 $ CD $。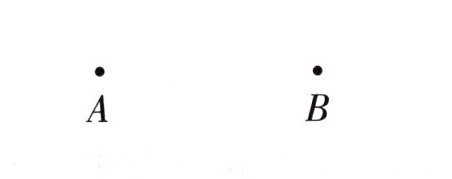

画图步骤：用直尺连接A、B两点得到直线l；将圆规两脚分别固定在A、B两点，保持圆规两脚间距离不变，在直线l上任取一点C，以C为圆心，用圆规画弧交直线l于点D，线段CD即为所求

答案： 1. 1
2. （画图步骤：用直尺连接A、B两点得到直线l；将圆规两脚分别固定在A、B两点，保持圆规两脚间距离不变，在直线l上任取一点C，以C为圆心，用圆规画弧交直线l于点D，线段CD即为所求）

4. 用圆规量一量蚂蚁从点 $ A $ 到点 $ F $ 的两条路线,哪条路线比较长？

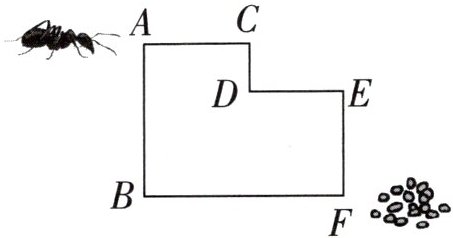
答案： 两条路线同样长，作答如下：
假设圆规两脚间距离为一定长度，从点$A$开始，沿折线$A - C - D - E - F$依次量取：
设圆规一脚在$A$点，另一脚拉到能刚好走到$C$点，记录圆规跨距次数；继续以同样方式从$C$点到$D$点、$D$点到$E$点、$E$点到$F$点，记录总跨距次数。
同样，用圆规从点$A$开始，沿直线$A - B - F$依次量取，即从$A$点到$B$点，再从$B$点到$F$点，记录总跨距次数。
经测量，沿折线$A - C - D - E - F$和沿直线$A - B - F$的圆规跨距次数相同。
所以两条路线长度相等。

兰兰做了两个不同形状的框架(如下图),哪个框架需要的木条更长？(请你用圆规比一比)

答案： 用圆规比较左图中长方形四条边的长度，设长边为a和b，短边为c和d，经比较a = b，c = d，且两条长边长于两条短边，总长度为2a + 2c。
用圆规比较右图中平行四边形的四条边，设上边为e，斜边为f、g、h，经比较e与对边相等，f、g、h、（另一条与f相对的边）四条边中斜边长度均相等且长于上边长度，总长度为2e + 2f，且f长于c，a长于e，2a + 2c与2e + 2f中，a与f（或平行四边形其他斜边）比较时f更长，c与e比较时c更长的情况不存在（实际e短于a，f长于c），整体比较平行四边形四条边总长度更长。
所以平行四边形框架需要的木条更长。