第90页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
我知道了不同的球从同一高度自由落下,反弹高度(
不同
);同一种球从不同高度自由落下,反弹高度(不同
)。
答案:
不同;不同
打篮球、踢足球、拍皮球等都是同学们喜爱的运动。这些球从高处落地后都会反弹。在正常情况下,球的反弹高度大约是下落高度的几分之几?各种不同的球的反弹情况相同吗?
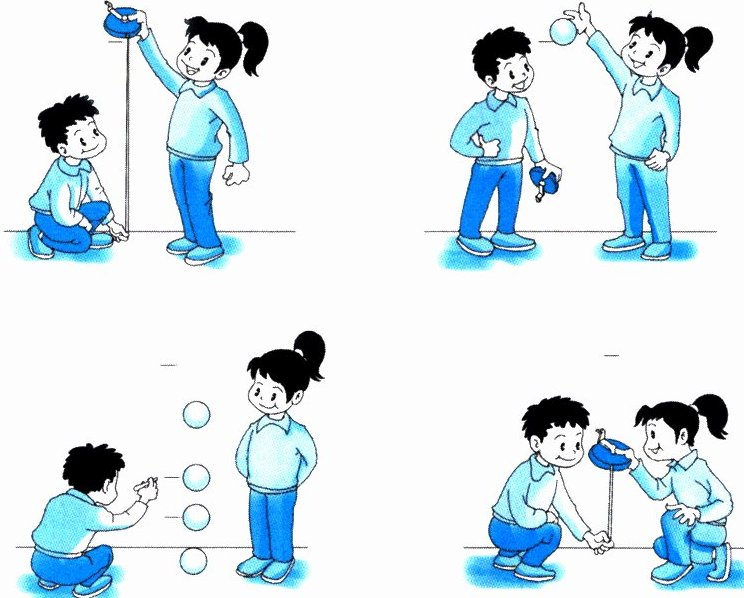

答案:
在正常情况下,不同球的反弹高度大约是下落高度的几分之几不同,各种不同的球的反弹情况不相同。
1. 用同一个球做实验,并记录。
实验记录(以篮球为例)
|(篮球)球|第一次|第二次|第三次|
| ---- | ---- | ---- | ---- |
|下落高度/cm|100|120|150|
|反弹高度/cm|65|78|97.5|
|反弹高度是下落高度的几分之几|$\frac{65}{100}=\frac{13}{20}$|$\frac{78}{120}=\frac{13}{20}$|$\frac{97.5}{150}=\frac{13}{20}$|
2. 交流反思。
(1) 和你的朋友交流一下实验的数据和发现。
(2) 在活动中,你有什么收获?遇到了哪些困难?是如何解决的?
收获:通过实验,更直观地理解了分数在实际情境(反弹高度与下落高度关系)中的应用,提高了动手操作能力和观察能力。
困难:在测量反弹高度时,球反弹速度较快,很难准确读取反弹高度的数值。
解决:多次重复实验,并且采用慢动作拍摄(如果有条件)或者找多个同学帮忙观察,取平均值来确定反弹高度。
(3) 还有哪些想要研究的问题?

3. 小结。
不同的球从同一个高度落下,其反弹高度一般是不同的,因此表示相应反弹高度与下落高度关系的分数自然也就不同。
4. 你知道吗?
球的弹性主要取决于球内部所受到的压力,而压力的大小与球内充进的空气多少有关。正式进行的球类比赛,对球的弹性都有明确的要求。例如,比赛用的篮球,从 1.8 m 的高度自由落下后,第一次反弹的高度应大于 1.2 m 且小于 1.4 m。
5. 自我评价。

实验记录(以篮球为例)
|(篮球)球|第一次|第二次|第三次|
| ---- | ---- | ---- | ---- |
|下落高度/cm|100|120|150|
|反弹高度/cm|65|78|97.5|
|反弹高度是下落高度的几分之几|$\frac{65}{100}=\frac{13}{20}$|$\frac{78}{120}=\frac{13}{20}$|$\frac{97.5}{150}=\frac{13}{20}$|
2. 交流反思。
(1) 和你的朋友交流一下实验的数据和发现。
和朋友交流时,发现不同的球(如篮球和乒乓球)从相同高度下落,反弹高度不同。以记录的篮球数据为例,每次下落高度改变,反弹高度也改变,但反弹高度与下落高度的比值大致相同(这里是$\frac{13}{20}$)。
(2) 在活动中,你有什么收获?遇到了哪些困难?是如何解决的?
收获:通过实验,更直观地理解了分数在实际情境(反弹高度与下落高度关系)中的应用,提高了动手操作能力和观察能力。
困难:在测量反弹高度时,球反弹速度较快,很难准确读取反弹高度的数值。
解决:多次重复实验,并且采用慢动作拍摄(如果有条件)或者找多个同学帮忙观察,取平均值来确定反弹高度。
(3) 还有哪些想要研究的问题?
除了足球落下高度和反弹高度的关系、影响反弹高度的因素外,还想研究不同材质的球(如橡胶球和皮革球)从相同高度下落,反弹高度的差异以及原因;球的充气量不同(在一定范围内)对反弹高度的具体影响规律等。

3. 小结。
不同的球从同一个高度落下,其反弹高度一般是不同的,因此表示相应反弹高度与下落高度关系的分数自然也就不同。
4. 你知道吗?
球的弹性主要取决于球内部所受到的压力,而压力的大小与球内充进的空气多少有关。正式进行的球类比赛,对球的弹性都有明确的要求。例如,比赛用的篮球,从 1.8 m 的高度自由落下后,第一次反弹的高度应大于 1.2 m 且小于 1.4 m。
5. 自我评价。

答案:
1. 实验记录(以篮球为例)
|(篮球)球|第一次|第二次|第三次|
| ---- | ---- | ---- | ---- |
|下落高度/cm|100|120|150|
|反弹高度/cm|65|78|97.5|
|反弹高度是下落高度的几分之几|$\frac{65}{100}=\frac{13}{20}$|$\frac{78}{120}=\frac{13}{20}$|$\frac{97.5}{150}=\frac{13}{20}$|
2. 交流反思
(1)交流实验数据和发现**:和朋友交流时,发现不同的球(如篮球和乒乓球)从相同高度下落,反弹高度不同。以记录的篮球数据为例,每次下落高度改变,反弹高度也改变,但反弹高度与下落高度的比值大致相同(这里是$\frac{13}{20}$)。
(2)收获、困难及解决
收获:通过实验,更直观地理解了分数在实际情境(反弹高度与下落高度关系)中的应用,提高了动手操作能力和观察能力。
困难:在测量反弹高度时,球反弹速度较快,很难准确读取反弹高度的数值。
解决:多次重复实验,并且采用慢动作拍摄(如果有条件)或者找多个同学帮忙观察,取平均值来确定反弹高度。
(3)想要研究的问题**:除了足球落下高度和反弹高度的关系、影响反弹高度的因素外,还想研究不同材质的球(如橡胶球和皮革球)从相同高度下落,反弹高度的差异以及原因;球的充气量不同(在一定范围内)对反弹高度的具体影响规律等。
|(篮球)球|第一次|第二次|第三次|
| ---- | ---- | ---- | ---- |
|下落高度/cm|100|120|150|
|反弹高度/cm|65|78|97.5|
|反弹高度是下落高度的几分之几|$\frac{65}{100}=\frac{13}{20}$|$\frac{78}{120}=\frac{13}{20}$|$\frac{97.5}{150}=\frac{13}{20}$|
2. 交流反思
(1)交流实验数据和发现**:和朋友交流时,发现不同的球(如篮球和乒乓球)从相同高度下落,反弹高度不同。以记录的篮球数据为例,每次下落高度改变,反弹高度也改变,但反弹高度与下落高度的比值大致相同(这里是$\frac{13}{20}$)。
(2)收获、困难及解决
收获:通过实验,更直观地理解了分数在实际情境(反弹高度与下落高度关系)中的应用,提高了动手操作能力和观察能力。
困难:在测量反弹高度时,球反弹速度较快,很难准确读取反弹高度的数值。
解决:多次重复实验,并且采用慢动作拍摄(如果有条件)或者找多个同学帮忙观察,取平均值来确定反弹高度。
(3)想要研究的问题**:除了足球落下高度和反弹高度的关系、影响反弹高度的因素外,还想研究不同材质的球(如橡胶球和皮革球)从相同高度下落,反弹高度的差异以及原因;球的充气量不同(在一定范围内)对反弹高度的具体影响规律等。
查看更多完整答案,请扫码查看


