《2025年作业本浙江教育出版社三年级数学上册北师大版》

1. 算一算。
27+49÷7
78-4×8
36+36÷9

答案： 1.
$27 + 49 {÷} 7$
$=27 + 7$
$= 34$
2.
$78 - 4 × 8$
$= 78 - 32$
$= 46$
3.
$36 + 36 {÷} 9$
$= 36 + 4$
$= 40$

2. 看图列算式。
(1) 还剩几元？
______
(2) 两种手套每双价格相差几元？
______

答案：
(1) $41 - 7× 3$
$= 41 - 21$
$= 20$(元)
答：还剩20元。
(2) $32÷ 4 - 14÷ 2$
$= 8 - 7$
$= 1$(元)
或$(32 - 14× 2)÷ 4$
$= (32 - 28)÷ 4$
$= 4÷ 4$
$= 1$(元)
答：两种手套每双价格相差1元。

3.

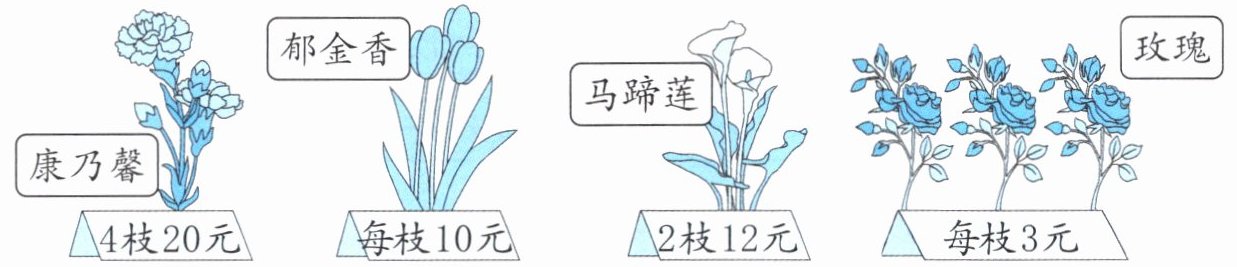
(1) 一枝玫瑰比一枝马蹄莲便宜多少元？
(2) 买一枝郁金香和一枝康乃馨,一共要多少元？

答案：
(1)
马蹄莲单价：$12÷2 = 6$（元）
一枝玫瑰比一枝马蹄莲便宜：$6 - 3 = 3$（元）
(2)
康乃馨单价：$20÷4 = 5$（元）
买一枝郁金香和一枝康乃馨一共：$10 + 5 = 15$（元）

4. 在下面算式的□里分别填上3、6、12,使等式成立。
(1) □÷□+□= 5
(2) □-□÷□= 10

答案： 【解析】：
(1) 对于等式 □÷□+□= 5，我们可以尝试将3、6、12填入等式，验证等式是否成立。
尝试组合：
当第一个□填12，第二个□填6，第三个□填3时，等式变为 12÷6+3=5，等式成立。
当其他组合时，等式均不成立。
因此，第一个等式的解为：12÷6+3= 5。
(2) 对于等式 □-□÷□= 10，我们同样尝试将3、6、12填入等式，验证等式是否成立。
尝试组合：
当第一个□填12，第二个□填12，第三个□填6时，等式变为 12-12÷6=10，等式成立（注意运算顺序，先除后减）。
当其他组合时，等式均不成立。
另外，考虑到除数不能为0，且要保证等式有意义，我们需检查所有可能的除数组合，这里已涵盖所有有效组合。
因此，第二个等式的解为：12-12÷6= 10，也可以写成等价形式 6×(2-1)=12-6=10-0(这里0是隐含的，因为12-12÷6=12-2×6÷6=12-2=10)，但直接形式 12-12÷6= 10 是最简洁的。
【答案】：
(1) 12；6；3
(2) 12；12；6