《2025年单元学习指导与练习九年级数学上册浙教版》

 【变式】如图1-5所示,四边形ABCD是菱形,点D的坐标是(0,$\sqrt{3}$),以C为顶点的抛物线$y = ax^2+bx + c$恰好经过x轴上的A,B两点.

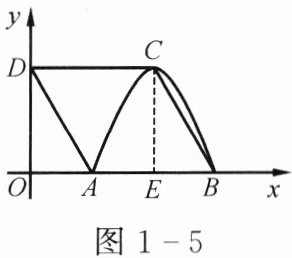
(1)求A,B,C三点的坐标.
(2)求过A,B,C三点的抛物线的函数表达式.
(3)若上述抛物线沿其对称轴向上平移后恰好经过点D,求平移后抛物线的函数表达式,并指出平移了多少个单位长度.

答案：
$(1) $设菱形边长为$m，$点$C$坐标为$(n, √3)。$因$D(0,√3)，$故$CD=n，$$AD=√(OA²+OD²)=√(OA²+3)=m，$即$OA²+3=m²。$抛物线以$C$为顶点，对称轴为$x=n，$$A、$$B$在$x$轴上且关于对称轴对称，设$A(n - t, 0)，$$B(n + t, 0)。$$AD=CD=m，$$AD²=(n - t)² + (√3)²=m²，$$CD²=n²=m²，$故$(n - t)² + 3 = n²，$得$t² - 2nt + 3=0。$又$AB=2t，$$AC=√(t² + 3)=m=n，$即$t² + 3 = n²，$结合$t² - 2nt + 3=0，$得$n² - 2nt = 0，$$n≠0，$故$n=2t，$$t² + 3=4t²，$$t=1，$$n=2，$$A(1,0)，$$B(3,0)，$$C(2,√3)。$　　
$(2) $抛物线顶点$C(2,√3)，$设$y=a(x - 2)² + √3，$过$A(1,0)，$$0=a(1 - 2)² + √3，$$a=-√3，$表达式$y=-√3(x - 2)² + √3。$　　
$(3) $原抛物线$y=-√3(x - 2)² + √3，$向上平移$k$个单位得$y=-√3(x - 2)² + √3 + k，$过$D(0,√3)，$$√3=-√3(0 - 2)² + √3 + k，$$k=4√3，$平移后表达式$y=-√3(x - 2)² + 5√3，$平移$4√3$个单位。　　
答案：　　
$(1)A(1,0)，$$B(3,0)，$$C(2,√3)；$　　
$(2)y=-√3(x - 2)² + √3；$　　
$(3)$平移后表达式$y=-√3(x - 2)² + 5√3，$平移$4√3$个单位。　　

例4 如图1-6所示,抛物线$y= \frac{1}{2}x^2 + bx - 2$与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(-1,0).

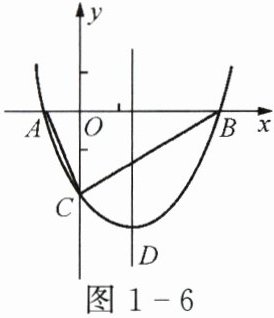
(1)求抛物线的函数表达式及顶点D的坐标.
(2)试判断△ABC的形状,并证明你的结论.
(3)M(m,0)是x轴上的一个动点,当$CM + DM$的值最小时,求m的值.

答案：
(1)
∵点A(-1,0)在抛物线$y= \frac{1}{2}x^2 + bx - 2$上,
∴$\frac{1}{2}×(-1)^2 + b×(-1)-2 = 0$,解得$b= -\frac{3}{2}$,
∴抛物线的函数表达式为$y= \frac{1}{2}x^2-\frac{3}{2}x - 2$.
$y= \frac{1}{2}x^2-\frac{3}{2}x - 2= \frac{1}{2}(x^2 - 3x - 4)= \frac{1}{2}(x-\frac{3}{2})^2-\frac{25}{8}$,
∴顶点D的坐标为($\frac{3}{2},-\frac{25}{8}$).
(2)△ABC是直角三角形.
证明：当$x = 0$时,$y= -2$,
∴C(0,-2),$OC = 2$.
当$y = 0$时,$\frac{1}{2}x^2-\frac{3}{2}x - 2 = 0$,解得$x_1= -1$,$x_2 = 4$,
∴B(4,0).
∴$OA = 1$,$OB = 4$,$AB = 5$.
∵$AB^2 = 25$,$AC^2= OA^2 + OC^2 = 1^2 + 2^2= 5$,$BC^2= OC^2 + OB^2 = 2^2 + 4^2= 20$,
∴$AC^2 + BC^2= 5 + 20=25= AB^2$.
∴△ABC是直角三角形.
(3)记点C关于x轴的对称点为$C'$,则$C'(0,2)$.
设直线$C'D$的函数表达式为$y = kx + n$,
∵$C'(0,2)$，$D(\frac{3}{2},-\frac{25}{8})$,
∴$\begin{cases}n = 2\frac{3}{2}k + n= -\frac{25}{8}\end{cases}$,解得$\begin{cases}n = 2\\k= -\frac{41}{12}\end{cases}$.
∴直线$C'D$的函数表达式为$y= -\frac{41}{12}x + 2$.
当$y = 0$时,$-\frac{41}{12}x + 2 = 0$,解得$x= \frac{24}{41}$.
∴$m= \frac{24}{41}$.