1. 描出下列各点,并依次连成封闭图形,看看是什么图形。
$A(5,9)$ $B(3,6)$ $C(5,3)$ $D(7,6)$
$A(5,9)$ $B(3,6)$ $C(5,3)$ $D(7,6)$

答案:
在方格图中:
点A(5, 9)位于第5列第9行。
点B(3, 6)位于第3列第6行。
点C(5, 3)位于第5列第3行。
点D(7, 6)位于第7列第6行。
依次连接A、B、C、D四点形成封闭图形。
计算各边长度:
$AB=\sqrt{(5 - 3)^2+(9 - 6)^2}=\sqrt{4 + 9}=\sqrt{13}$。
$BC=\sqrt{(5 - 3)^2+(3 - 6)^2}=\sqrt{4 + 9}=\sqrt{13}$。
$CD=\sqrt{(7 - 5)^2+(6 - 3)^2}=\sqrt{4 + 9}=\sqrt{13}$。
$DA=\sqrt{(7 - 5)^2+(9 - 6)^2}=\sqrt{4 + 9}=\sqrt{13}$。
四条边长度都为$\sqrt{13}$,是菱形,又因为对角线$AC$在竖直方向,$BD$在水平方向,$AC\perp BD$,所以该图形是菱形(特殊的长方形相关图形,在本题按边判断也可知是菱形)。
答:依次连成封闭图形是菱形。
点A(5, 9)位于第5列第9行。
点B(3, 6)位于第3列第6行。
点C(5, 3)位于第5列第3行。
点D(7, 6)位于第7列第6行。
依次连接A、B、C、D四点形成封闭图形。
计算各边长度:
$AB=\sqrt{(5 - 3)^2+(9 - 6)^2}=\sqrt{4 + 9}=\sqrt{13}$。
$BC=\sqrt{(5 - 3)^2+(3 - 6)^2}=\sqrt{4 + 9}=\sqrt{13}$。
$CD=\sqrt{(7 - 5)^2+(6 - 3)^2}=\sqrt{4 + 9}=\sqrt{13}$。
$DA=\sqrt{(7 - 5)^2+(9 - 6)^2}=\sqrt{4 + 9}=\sqrt{13}$。
四条边长度都为$\sqrt{13}$,是菱形,又因为对角线$AC$在竖直方向,$BD$在水平方向,$AC\perp BD$,所以该图形是菱形(特殊的长方形相关图形,在本题按边判断也可知是菱形)。
答:依次连成封闭图形是菱形。
2. 下图是某游乐城的一角。

(1) 用数对表示各游乐点所在的位置。
摩天轮(
攀岩(
(2) 鬼城在$(7,5)$,空中飞船在$(2,6)$,请在图中标出鬼城和空中飞船的位置。
(3) 从探险洞出发,向西走 200 m,再向南走 150 m 到达碰碰车处,请在图中标出碰碰车的位置。

(1) 用数对表示各游乐点所在的位置。
摩天轮(
2
,7
) 探险洞(6
,6
)攀岩(
3
,3
) 迷宫(8
,4
)(2) 鬼城在$(7,5)$,空中飞船在$(2,6)$,请在图中标出鬼城和空中飞船的位置。
(3) 从探险洞出发,向西走 200 m,再向南走 150 m 到达碰碰车处,请在图中标出碰碰车的位置。
答案:
(1)(2,7) (6,6) (3,3) (8,4)
(2)略 (3)略
(2)略 (3)略
3. 先写出三角形$ABC$各个顶点的位置,再画出三角形$ABC$向下平移 4 格后的三角形$A'B'C'$,最后写出所得图形顶点的位置。
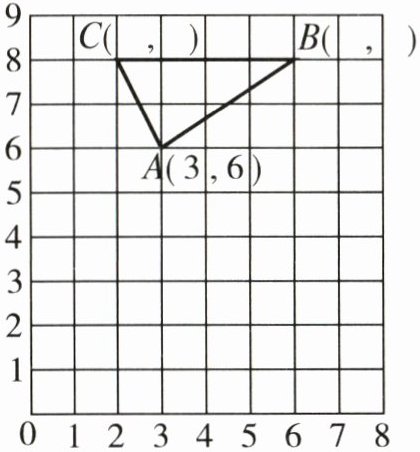
$B($

$B($
6
,8
$)$ $C($2
,8
$)$ $A'($3
,2
$)$ $B'($6
,4
$)$ $C'($2
,4
$)$
答案:
B(6,8) C(2,8) A'(3,2) B'(6,4) C'(2,4) 图略
查看更多完整答案,请扫码查看


