《2025年经纶学典学霸课时作业二年级数学上册人教版》

$36+17= $
$94-28= $
$25+48= $
$70-35= $
$19+63= $
$81-47= $
$52+29= $
$77-19= $
$44+38= $
$99-65= $

答案： 53 66 73 35 82 34 81 58 82 34

1. 新趋势 算理理解 一共有多少只蜜蜂？
(1)竖着看,每列有( )只,有这样的( )列。
加法算式：______
乘法算式：______
(2)横着看,每行有( )只,有这样的( )行。
加法算式：______
乘法算式：______
(3)我发现：交换乘数的位置( )(填“影响”或“不影响”)积的大小。

答案： 1.
(1)5 3 5+5+5=15
5×3=15
(2)3 5 3+3+3+3+3=15
3×5=15
(3)不影响

2. 按要求画一画,再计算。
(1)每组画3个○,画3组。 □
加法算式：______
乘法算式：______
(2)每组画2个△,画5组。 □
加法算式：______
乘法算式：______

答案： 2.
(1)
加法算式：3+3+3=9
乘法算式：3×3=9
(2)△△
△△
△△
△△
△△
加法算式：2+2+2+2+2=10
乘法算式：2×5=10

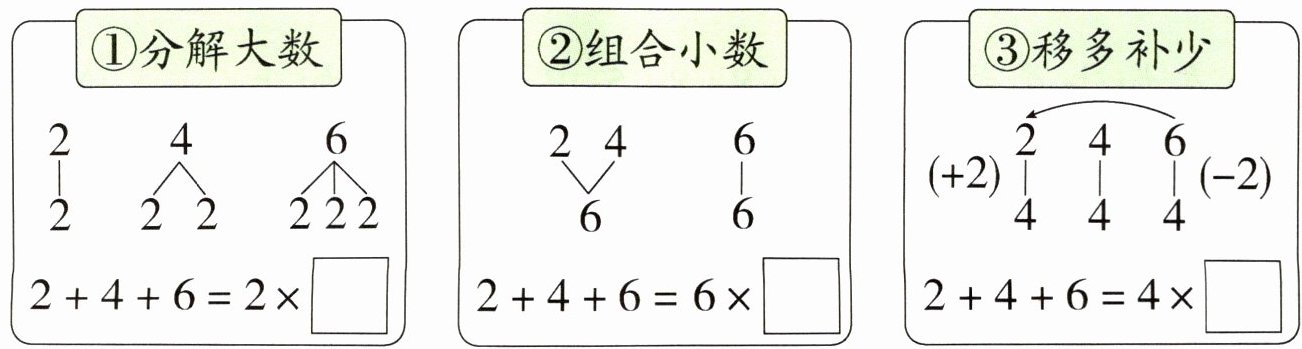
3. 下面是改写算式$2+4+6$的三种方法,请你补充完整。
①分解大数
2 4 6
2 2 2 2 2 2
$2+4+6= 2×□$
②组合小数
2 4 6
6 6
$2+4+6= 6×□$
③移多补少
2 4 6
(+2) 4 4 4 (-2)
$2+4+6= 4×□$

答案： 3. 6 2 3
提示:①分解大数策略下的转化:对于加法算式2+4+6。我们观察到数字4,可以把它分解成2+2,这就等同于有2个2。再看数字6,它能够分解成2+2+2,也就意味着有3个2。原本还有1个2,那么2的总数就是1+2+3=6(个)。根据乘法的定义,乘法是求几个相同加数和的简便运算，这里是6个2相加，所以可以写成乘法算式2×6。
②组合小数策略下的转化:针对加法算式2+4+6。我们发现可以把较小的数2和4组合起来，即2+4=6。这样就得到了1个新的6,再加上原来就有的1个6,总共就有2个6。依据乘法的意义,2个6相加可以用乘法算式6×2来表示。
③移多补少策略下的转化:在加法算式2+4+6里,最大的数是6,它比4多的数量为6−4=2;最小的数是2,它比4少的数量为4−2=2。我们采取移多补少的方法,把6减少2使其变为4,把2增加2也变为4。此时就形成了3个4,按照乘法的意义,3个4相加能够写成乘法算式4×3。