《2025年经纶学典提高班五年级数学上册苏教版》

1. 下面两个平行四边形的面积都是20平方厘米,分别写出涂色部分的面积。


(1)10平方厘米
(2)10平方厘米

答案： 1.
(1)10
(2)10
提示:
(1)中涂色三角形的底的长度等于平行四边形的底的长度，高的长度之和等于平行四边形的高的长度，所以涂色三角形的面积和是平行四边形面积的一半。
(2)与
(1)同理可得涂色部分面积是平行四边形面积的一半。

2. 如图,梯形ABCD中,E、F分别是腰AB、DC的中点,G、H是AD、BC上任意一点。已知梯形ABCD的面积是42平方厘米,写出涂色部分的面积。

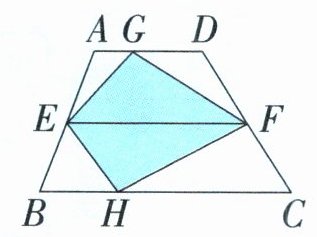
答案： 42÷2=21(平方厘米)
答:涂色部分的面积是21平方厘米。
提示:将两个这样的梯形拼到一起，根据我们之前例题中的推导可以得到涂色部分的面积是平行四边形ABA'B'面积的一半，所以涂色部分的面积是梯形ABCD面积的一半。

3. 如图,在梯形ABCD中,E、F分别是腰AB、CD的中点$,S_1$和$S_2$的大小分别是8和18。求梯形ABCD的面积。

答案： 3.(8+18)×2×2=104
答:梯形ABCD的面积是104。
提示:将两个这样的梯形拼到一起，如图，根据例题中的推导可以得到涂色部分的面积是平行四边形ABA'B'面积的一半，所以S₁+S₂+S₃+S₄的面积和的2倍也是平行四边形ABA'B'面积的一半。又因为三角形AEP和三角形BEP同底等高，三角形DPF和三角形CPF同底等高，所以S₁=S₃,S₂=S₄,所以S₁+S₂+S₃+S₄=2×(S₁+S₂)=2×(8+18)=52,梯形ABCD的面积就是52×2=104。