《2025年小学学霸作业本五年级数学上册苏教版江苏专版》

1. 晓晨、张宇、子怡、徐明是好朋友,如果他们每两人之间视频一次,一共要视频多少次？如果他们互相发一条短信,一共要发多少条短信？

答案： 解析：
本题考查的是组合的问题。
已知晓晨、张宇、子怡、徐明是好朋友，他们每两人之间都要视频一次。
考虑第一个人晓晨，他需要和其他三人（张宇、子怡、徐明）视频，所以视频3次；
接着，考虑第二个人张宇，他已经和晓晨视频过了，所以他还需要和剩下的两人（子怡、徐明）视频，再视频2次；
然后，第三个人子怡，他已经和晓晨、张宇都视频过了，所以他只需要和最后一个人（徐明）视频，视频1次；
最后，第四个人徐明，他已经和前面的三人都视频过了，所以不需要再视频。
因此，总共的视频次数为：3 + 2 + 1 = 6（次）。
如果他们互相发一条短信，则每个人都需要和其他三人各发一条短信。
所以，每个人发3条，四人一共发：4 × 3 = 12（条）。
答案：
一共要视频6次；一共要发12条短信。

2. 姑苏区要举行小学生篮球赛,最后进入决赛的有5支球队。如果每两支球队比赛一场,一共要比赛多少场？

答案： 解析：本题考查组合问题，由于每两支球队之间只比赛一场，因此可以避免重复计算。
可以通过组合的方式计算出比赛场数，即$C_{5}^2$。
$C_{5}^2=\frac{5×4}{2×1}=10$。
也可以通过列举法来解答。
假设5支球队分别为A, B, C, D, E。
那么比赛组合可以为：
A与B，A与C，A与D，A与E
B与C，B与D，B与E（B与A已在上面列出，所以不再重复）
C与D，C与E（C与A、B已在上面列出，所以不再重复）
D与E（D与A、B、C已在上面列出，所以不再重复）
这样列举出来，一共也是10场比赛。
答案：一共要比赛10场。

3. 用0、3、7三个数字和小数点一共可以组成多少个不同的两位小数？

答案： 0.37、0.73、3.07、3.70、7.03、7.30
一共可以组成6个不同的两位小数。

4. 下图中有多少个长方形？

答案： 先数长边上线段数：4+3+2+1=10（条）
再数宽边上线段数：2+1=3（条）
长方形总数：10×3=30（个）
答：图中有30个长方形。

5. 在下面的图形中,再涂1个格子,使涂色部分成为一个轴对称图形,有几种不同的涂法？

答案： 1. 横向对称轴：对称轴为第3行，已有涂色格子在(3,3)、(4,2)、(4,4)，需在(2,3)处涂色。
2. 纵向对称轴：对称轴为第3列，已有涂色格子在(3,3)、(4,2)、(4,4)，需在(3,3)对称点已存在，无需额外涂色。
3. 左上-右下对角线对称轴：对称轴为从(1,1)到(5,5)对角线，已有涂色格子对称点分析，需在(2,2)处涂色。
4. 右上-左下对角线对称轴：对称轴为从(1,5)到(5,1)对角线，已有涂色格子对称点分析，需在(2,4)处涂色。
结论：有3种不同的涂法。

6. 小军、小强和小宇玩套圈游戏,套中跳跳虎得5分,套中长颈鹿得4分,套中大象得3分。小军套中1次,可能得多少分？小强套中2次,可能得多少分？小宇套中3次,可能得多少分？

答案： 小军套中1次：5分，4分，3分。
小强套中2次：10分（5+5），9分（5+4），8分（5+3或4+4），7分（4+3），6分（3+3）。
小宇套中3次：15分（5+5+5），14分（5+5+4），13分（5+5+3或5+4+4），12分（5+4+3或4+4+4），11分（5+3+3或4+4+3），10分（4+3+3），9分（3+3+3）。

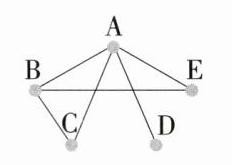
7. 在篮球比赛中,每赢一球,队员都会以击掌来表示庆贺。如图,五名队员中,A击了4次掌,B击了3次掌,C击了2次掌,D击了1次掌,E击了几次掌？分别是和谁击的掌呢？

答案：
解析：这是一道关于逻辑推理和列举策略的题目，解题的关键在于根据每个队员击掌的次数，通过分析不同队员之间可能的击掌组合来确定$E$击掌的次数和对象。
从击掌次数最少的$D$开始分析，$D$击了$1$次掌，因为$D$只可能和其他队员击掌，所以$D$这一掌是和$A$、$B$、$C$、$E$中的某一位击的。
再看$A$击了$4$次掌，这意味着$A$和$B$、$C$、$D$、$E$都击了掌。
$B$击了$3$次掌，由于已经确定$A$和$B$击过掌，$D$只击了$1$次掌且是和$A$击的，所以$B$剩下的$2$次掌是和$C$、$E$击的。
$C$击了$2$次掌，由前面的推理可知$C$这$2$次掌是和$A$、$B$击的。
通过以上分析，$E$和$A$击了一次掌，又因为$B$还剩下一次掌是和$E$击的，所以$E$一共击了$2$次掌，分别是和$A$、$B$击的。
答案：$E$击了$2$次掌，分别是和$A$、$B$击的掌。